المحاضرة 5/ القطع المكافئ – ايجاد المجهول

المعادلة المعطاة:

$a x^2 + 4y = 0$

نحولها إلى الصيغة القياسية:

$4y = -a x^2$ $y = -\frac{a}{4} x^2$

وهذه معادلة قطع مكافئ رأسي مفتوح لأسفل من الشكل:

$y = \frac{1}{4p} x^2$

بمقارنة المعادلتين نجد أن:

$\frac{1}{4p} = -\frac{a}{4}$

أي:

$p = -\frac{1}{a}$

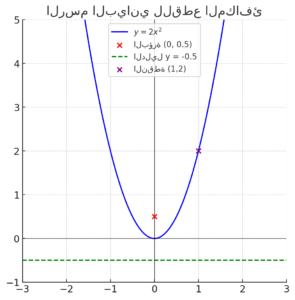
بما أن القطع المكافئ يمر بالنقطة $(1,1)$ ، فإننا نعوض بها في المعادلة:

$1 = -\frac{a}{4} (1)^2$ $1 = -\frac{a}{4}$ $a = -4$

$y = \frac{4}{4} x^2$ $y = -x^2$

نعرف أن البؤرة تكون عند:

$(0, p)$

وأن الدليل يكون:

$y = -p$

بما أن:

$p = -\frac{1}{a} = -\frac{1}{-4} = \frac{1}{4}$

إذن البؤرة:

$\left( 0, \frac{1}{4} \right)$

والدليل:

$y = -\frac{1}{4}$

السؤال التالي

المعادلة المعطاة للقطع المكافئ هي:

$a x^2 + 8y = 0$

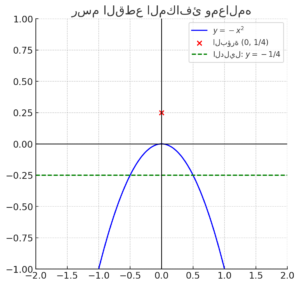
بما أن القطع يمر بالنقطة $(1,2)$ ، فإن هذه النقطة تحقق المعادلة:

$a(1)^2 + 8(2) = 0$ $a + 16 = 0$ $a = -16$

إذن، معادلة القطع المكافئ تصبح:

$-16x^2 + 8y = 0$ $8y = 16x^2$ $y = 2x^2$

وهي على الصورة القياسية:

$y = 4p x^2$

بالمقارنة مع المعادلة القياسية $y = 4p x^2$ ، نجد أن:

$4p = 2$ $p = \frac{1}{2}$

إحداثيات البؤرة: تكون البؤرة على بعد $p$ من الرأس (نقطة الأصل)، أي أن إحداثياتها:
$F \left( 0, \frac{1}{2} \right)$
معادلة الدليل: يكون الدليل على بعد $p$ في الاتجاه المعاكس للبؤرة، أي أن معادلته:
$y = -\frac{1}{2}$