انسحاب المحاور للقطع المكافئ / الجزء الثاني

الرياضيات للصف السادس العلمي انسحاب المحاور للقطع المكافئ / الجزء الثاني

 

السؤال المكتوب في الصورة هو:

جد البؤرة والدليل والرأس ومعادلة المحور للقطع المكافئ:
y=x2+4xy = x^2 + 4x

لحل المعادلة وإيجاد البؤرة والدليل والرأس ومعادلة المحور للقطع المكافئ:

1. إعادة كتابة المعادلة في الصورة القياسية

المعادلة المعطاة هي:

y=x2+4xy = x^2 + 4x

نحتاج إلى إكمال المربع لوضعها في الصورة القياسية:

y=(x2+4x)+0y = (x^2 + 4x) + 0

لإكمال المربع، نضيف ونطرح (4/2)^2 = 4 داخل القوس:

y=(x2+4x+4)−4y = (x^2 + 4x + 4) – 4 y=(x+2)2−4y = (x + 2)^2 – 4

الصيغة القياسية للقطع المكافئ الرأسي هي:

y=(x−h)2+ky = (x – h)^2 + k

بمقارنة المعادلة لدينا مع هذه الصيغة، نجد أن:

  • رأس القطع المكافئ هو (-2, -4).

2. إيجاد البؤرة

معادلة القطع المكافئ في الصورة القياسية:

(y−k)=a(x−h)2(y – k) = a(x – h)^2

حيث أن البعد البؤري يعطى بالعلاقة 14c\frac{1}{4c}، ولدينا:

y=(x+2)2−4y = (x + 2)^2 – 4

نقارنها مع:

y=a(x−h)2+ky = a(x – h)^2 + k

حيث a=1a = 1 و h=−2h = -2 و k=−4k = -4.

البعد البؤري يُحسب من العلاقة:

4c=1a=11=44c = \frac{1}{a} = \frac{1}{1} = 4

إذن:

c=14a=14=14c = \frac{1}{4a} = \frac{1}{4} = \frac{1}{4}

البؤرة تقع على بعد cc من الرأس على طول محور التماثل yy، أي:

(−2,−4+14)(-2, -4 + \frac{1}{4}) (−2,−154)(-2, -\frac{15}{4})

3. إيجاد معادلة الدليل

معادلة الدليل تعطى بالعلاقة:

y=k−cy = k – c y=−4−14y = -4 – \frac{1}{4} y=−174y = -\frac{17}{4}

4. معادلة محور التماثل

محور التماثل هو الخط العمودي المار بالرأس:

x=−2x = -2

الإجابة النهائية

  • الرأس: (−2,−4)(-2, -4)
  • البؤرة: (−2,−154)(-2, -\frac{15}{4})
  • معادلة الدليل: y=−174y = -\frac{17}{4}
  • معادلة محور التماثل: x=−2x = -2

السؤال :

جد البؤرة والدليل والرأس ومعادلة المحور للقطع المكافئ
8y+7=x2+2x8y + 7 = x^2 + 2x
ثم ارسمه.

لحل المعادلة وإيجاد البؤرة، الدليل، الرأس، ومعادلة المحور للقطع المكافئ المعطى:

1. تحويل المعادلة إلى الصورة القياسية

المعادلة المعطاة هي:

8y+7=x2+2x8y + 7 = x^2 + 2x

نطرح 7 من الطرفين:

8y=x2+2x−78y = x^2 + 2x – 7

نقسم على 8:

y=18(x2+2x−7)y = \frac{1}{8} (x^2 + 2x – 7)

2. إكمال المربع لتحويلها إلى الصورة القياسية

لدينا الجزء التربيعي:

x2+2xx^2 + 2x

نُكمل المربع بإضافة وطرح (22)2=1\left(\frac{2}{2}\right)^2 = 1:

x2+2x+1−1=(x+1)2−1x^2 + 2x + 1 – 1 = (x + 1)^2 – 1

نعوّض في المعادلة:

y=18((x+1)2−1−7)y = \frac{1}{8} ((x+1)^2 – 1 – 7) y=18(x+1)2−88y = \frac{1}{8} (x+1)^2 – \frac{8}{8} y=18(x+1)2−1y = \frac{1}{8} (x+1)^2 – 1

الصورة القياسية للقطع المكافئ:

y=18(x+1)2−1y = \frac{1}{8} (x + 1)^2 – 1

وهي على الصورة:

y=a(x−h)2+ky = a (x – h)^2 + k

حيث:

  • الرأس (h, k): (−1,−1)(-1, -1)
  • a = 18\frac{1}{8}، وهو موجب، مما يعني أن القطع المكافئ مفتوح للأعلى.

3. إيجاد البؤرة ومعادلة الدليل

في القطع المكافئ من الشكل y=a(x−h)2+ky = a(x – h)^2 + k، يكون البعد البؤري:

p=14a=14×18=148=84=2p = \frac{1}{4a} = \frac{1}{4 \times \frac{1}{8}} = \frac{1}{\frac{4}{8}} = \frac{8}{4} = 2

  • البؤرة: تتحقق عند (h,k+p)=(−1,−1+2)=(−1,1)(h, k + p) = (-1, -1 + 2) = (-1, 1).
  • معادلة الدليل: y=k−p=−1−2=−3y = k – p = -1 – 2 = -3

4. معادلة محور التماثل

محور التماثل هو الخط العمودي المار بالرأس:

x=−1x = -1

النتائج النهائية:

  • الرأس: (−1,−1)(-1, -1)
  • البؤرة: (−1,1)(-1, 1)
  • معادلة الدليل: y=−3y = -3
  • معادلة محور التماثل: x=−1x = -1

5. رسم القطع المكافئ

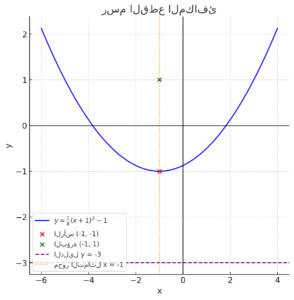
رسم القطع المكافئ
رسم القطع المكافئ

هذا هو الرسم البياني للقطع المكافئ y=18(x+1)2−1y = \frac{1}{8} (x+1)^2 – 1:

  • المنحنى الأزرق يمثل معادلة القطع المكافئ.
  • النقطة الحمراء هي الرأس عند (-1, -1).
  • النقطة الخضراء هي البؤرة عند (-1, 1).
  • الخط البنفسجي المتقطع يمثل معادلة الدليل y=−3y = -3.
  • الخط البرتقالي المنقط يمثل محور التماثل x=−1x = -1.

بهذا يكون السؤال قد تم حله بالكامل. 😊

المحاضرة السابق
رجوع إلى الدرس
المحاضرة التالي