السؤال:
الكتاب: من المعلومات المثبتة في الشكل، احسب:
- سعة المجموعة المكافئة
- الشحنة الكلية في المجموعة
- الشحنة المختزنة في أي من صفيحتي كل متسعة
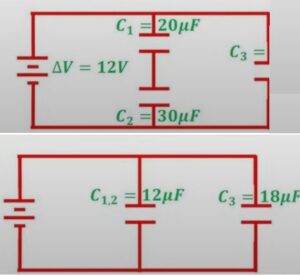 حل سؤال من الكتاب
حل سؤال من الكتاب
المعطيات من الشكل (الدائرة):
- ،
- ،
- وهما مربوطتان على التوازي ⇒
- الدائرة الكاملة: مربوطة على التوالي مع
- فرق الجهد الكلي:
الحل:
1. حساب السعة المكافئة:
2. حساب الشحنة الكلية:
3. حساب الشحنة في كل متسعة:
في التوازي:
- فرق الجهد متساوٍ عبر و:
أولاً نحسب :
إذًا:
- نحسب الشحنة على كل من و:
تحقق: ✅
الإجابات النهائية:
- السعة المكافئة للمجموعة:
- الشحنة الكلية في المجموعة:
- الشحنات في كل متسعة:

