أسئلة و امثلة حول حلول اسئلة تكاملات الدوال الشطرية
لحل أسئلة تكاملات الدوال الشطرية (Piecewise Functions Integration)، يمكن اتباع الخطوات التالية باختصار:
1. فهم تعريف الدالة الشطرية
- تأكد من أن لديك المعادلة الصحيحة للدالة مع الشروط المحددة لكل شطر.
- حدد الفواصل التي تتغير عندها الدالة.
2. تجزئة التكامل
- قم بتقسيم التكامل وفقًا للفواصل المحددة في تعريف الدالة الشطرية.
- كل شطر يُدمج على فترته الخاصة.
3. إجراء التكامل لكل شطر على حدة
- استخدم قواعد التكامل المعروفة (مثل التكامل المباشر، التكامل بالتجزئة، التكامل بالتعويض، إلخ) لكل جزء من الدالة.
4. جمع النتائج
- بعد إيجاد التكامل لكل شطر، اجمع القيم الناتجة للحصول على الحل النهائي.
5. التأكد من الشروط الحدية
- في حالة التكامل المحدد، تحقق من حدود التكامل وقم بتقييم القيم عندها.
- تأكد من أن القيم في النقاط التي يتغير عندها تعريف الدالة متسقة رياضيًا.
مثال توضيحي
إذا كانت لدينا الدالة الشطرية:
ونريد حساب التكامل المحدد:
نقسم التكامل إلى جزأين:
ثم نحسب كل جزء على حدة ونجمع النتيجة.
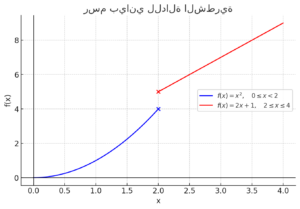 رسم بياني للدالة الشطرية
رسم بياني للدالة الشطرية
هذا هو الرسم البياني للدالة الشطرية. كما ترى، الدالة تتغير عند ، حيث يتغير تعريفها من إلى .
السؤال رقم 11:
إذا كان:
فأوجد:
الحل:
لحل التكامل، نحدد الفواصل التي تتغير عندها الدالة الشطرية:
- الدالة ثابتة عند عندما .
- الدالة خطية عندما .
نقسم التكامل إلى جزأين:
حساب التكامل الأول:
حساب التكامل الثاني:
نحسب كل جزء على حدة:
نجمع النتائج:
إجمالي التكامل:
الإجابة النهائية:
السؤال: رقم 12
إذا كان:
فأوجد:
الحل:
لحل التكامل، نقسمه إلى فترتين حيث تتغير الدالة عند :
حساب التكامل الأول:
حساب التكامل الثاني:
نحسب التكامل:
نطبق الحدود:
إجمالي التكامل:
الإجابة النهائية:
السؤال: رقم 13
لنكـن:
فأوجد:
الحل:
الدالة المعطاة هي الدالة المطلقة ، والتي تُعرَّف على جزأين:
بما أن التكامل يمتد من إلى ، نقسمه إلى جزأين عند النقطة الحرجة :
حساب التكامل الأول :
نطبق الحدود:
حساب التكامل الثاني :
نطبق الحدود:
إجمالي التكامل:
الإجابة النهائية:
السؤال:
أثبت أن:
الحل:
بما أن لدينا القيمة المطلقة ، نحدد متى يتغير سلوك الدالة.
1. إيجاد النقطة التي تجعل القيمة المطلقة صفرًا
لحل المعادلة :
إذن، تتغير الدالة عند ، لذا نقسم التكامل إلى جزأين:
2. تحليل القيمة المطلقة
نستخدم تعريف القيمة المطلقة:
3. حساب التكامل الأول
نحسب كل جزء:
نطبق الحدود إلى :
4. حساب التكامل الثاني
نحسب كل جزء:
نطبق الحدود إلى :
5. حساب الناتج الكلي
الإجابة النهائية:
وبذلك تم إثبات المطلوب! ✅
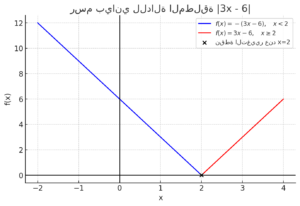 رسم بياني للدالة المطلقة
رسم بياني للدالة المطلقة
هذا هو الرسم البياني للدالة المطلقة . كما يظهر، تنقسم الدالة إلى جزأين:
- الجزء الأول (الأزرق): عندما حيث .
- الجزء الثاني (الأحمر): عندما حيث .
نقطة التغيير عند ، حيث تساوي .


