المسافة / محاضرة 33

التطبيقات الفيزيائية – حساب المسافة باستخدام التكامل

التكامل هو أداة رياضية قوية تُستخدم في الفيزياء لحساب العديد من الكميات مثل المسافة، الإزاحة، السرعة، والتسارع. في هذا الشرح، سنوضح كيف يمكن استخدام التكامل لحساب المسافة من خلال معرفة السرعة.

1. العلاقة بين المسافة والسرعة والتسارع

في الفيزياء، هناك علاقة مباشرة بين المسافة، السرعة، والتسارع:

• السرعة ($v(t)$): هي معدل تغير الموقع مع الزمن.
• الإزاحة ($s(t)$): هي الموضع بالنسبة لنقطة مرجعية.
• التسارع ($a(t)$): هو معدل تغير السرعة مع الزمن.

التكامل لحساب الإزاحة

إذا كانت لدينا دالة السرعة $v(t)$ كمشتقة لدالة الموقع $s(t)$، يمكننا إيجاد الإزاحة عن طريق التكامل:

$$s(t) = \int v(t) \, dt$$

حيث:

• $s(t)$ هو الموقع أو الإزاحة.
• $v(t)$ هو السرعة.

التكامل لحساب المسافة المقطوعة

المسافة تختلف عن الإزاحة، حيث تأخذ المسافة بعين الاعتبار مقدار الحركة بغض النظر عن الاتجاه. لذلك، تُحسب المسافة باستخدام القيمة المطلقة للسرعة:

$$\text{المسافة} = \int_{t_1}^{t_2} |v(t)| \, dt$$

أي أننا نأخذ القيمة المطلقة للسرعة لضمان أن المسافة لا تكون سالبة.

2. مثال عملي: حساب المسافة من دالة السرعة

مثال 1: حركة جسم بسرعة خطية

افترض أن جسمًا يتحرك وفق دالة السرعة:

$$v(t) = 3t^2 – 4t$$

ونريد حساب المسافة التي يقطعها الجسم بين الزمن $t = 0$ و $t = 3$.

الخطوات:

1. إيجاد فترات تغير الإشارة
   • لحساب المسافة، نحتاج إلى معرفة متى تتغير السرعة من موجبة إلى سالبة (أي متى يتوقف الجسم مؤقتًا).
   • نحل المعادلة: $v(t) = 0$ $$3t^2 – 4t = 0$$ $$t(3t – 4) = 0$$ $$t = 0 \quad \text{أو} \quad t = \frac{4}{3}$$
   • هذا يعني أن السرعة تتغير عند $t = 4/3$.
2. حساب المسافة باستخدام التكامل المجزأ
   • نكامل $|v(t)|$ في فترتين:
     1. الفترة $[0, 4/3]$، حيث $v(t)$ سالبة.
     2. الفترة $[4/3, 3]$، حيث $v(t)$ موجبة.
   • نحسب:

     $$\int_0^{4/3} |3t^2 – 4t| dt + \int_{4/3}^{3} (3t^2 – 4t) dt$$

   يمكنني الآن حساب القيمة الفعلية لهذا التكامل. سأقوم بحسابها رياضيًا.

بعد حساب التكامل، نجد أن المسافة الكلية التي يقطعها الجسم بين $t = 0$ و $t = 3$ هي تقريبًا:

$$\mathbf{11.37} \quad \text{وحدات المسافة}$$

وهذا يوضح كيف يمكن استخدام التكامل لحساب المسافة المقطوعة من دالة السرعة، مع الأخذ بعين الاعتبار تغير الإشارة عبر الفترات المختلفة.

شرح مفصل لحساب المسافة باستخدام التكامل – خطوة بخطوة

المطلوب:

لدينا دالة السرعة لجسم يتحرك:

$$v(t) = 3t^2 – 4t$$

ونريد حساب المسافة الكلية المقطوعة خلال الفترة $t \in [0, 3]$.

1. إيجاد لحظات توقف الجسم

• لحظات التوقف تحدث عندما تكون السرعة تساوي صفر، أي:

  $$v(t) = 0$$ $$3t^2 – 4t = 0$$

• نحلل المعادلة:

  $$t(3t – 4) = 0$$

• الحلول:

  $$t = 0 \quad \text{أو} \quad t = \frac{4}{3}$$

• إذن، يتوقف الجسم عند $t = 4/3$، مما يعني أن السرعة تتغير إشارتها عند هذه النقطة.

2. تحديد فترات السرعة الموجبة والسالبة

لحساب المسافة، يجب معرفة متى تكون $v(t)$ موجبة أو سالبة:

1. الفترة $[0, 4/3]$:
   • نختبر نقطة داخل الفترة، مثل $t = 1$:

   $$v(1) = 3(1)^2 – 4(1) = 3 – 4 = -1$$

   • إذن، السرعة سالبة في هذه الفترة، ولذلك نأخذ القيمة المطلقة عند التكامل.
2. الفترة $[4/3, 3]$:
   • نختبر نقطة داخل الفترة، مثل $t = 2$:

   $$v(2) = 3(2)^2 – 4(2) = 12 – 8 = 4$$

   • إذن، السرعة موجبة في هذه الفترة، فلا نحتاج للقيمة المطلقة.

3. حساب التكامل في كل فترة

الفترة $[0, 4/3]$ حيث السرعة سالبة:

نحسب:

$$\int_0^{4/3} |3t^2 – 4t| \, dt$$

بما أن السرعة سالبة، نضرب التكامل في -1 لجعل القيم موجبة:

$$\int_0^{4/3} (- (3t^2 – 4t)) \, dt$$

أي:

$$\int_0^{4/3} (4t – 3t^2) \, dt$$

نحسب التكامل:

$$\int (4t – 3t^2) \, dt = 2t^2 – t^3$$

نطبق الحدود:

$$\left[ 2t^2 – t^3 \right]_0^{4/3}$$

• عند $t = 4/3$:

  $$2(4/3)^2 – (4/3)^3 = 2(16/9) – (64/27)$$ $$= 32/9 – 64/27$$ $$= \frac{96}{27} – \frac{64}{27} = \frac{32}{27}$$

• عند $t = 0$:

  $$2(0)^2 – (0)^3 = 0$$

إذن:

$$\text{المسافة في الفترة الأولى} = \frac{32}{27} = 1.185$$

الفترة $[4/3, 3]$ حيث السرعة موجبة:

نحسب:

$$\int_{4/3}^{3} (3t^2 – 4t) \, dt$$

نفس التكامل السابق لكن بدون القيمة المطلقة:

$$\int (3t^2 – 4t) \, dt = t^3 – 2t^2$$

نطبق الحدود:

$$\left[ t^3 – 2t^2 \right]_{4/3}^{3}$$

• عند $t = 3$:

  $$3^3 – 2(3^2) = 27 – 18 = 9$$

• عند $t = 4/3$:

  $$(4/3)^3 – 2(4/3)^2 = (64/27) – 2(16/9)$$ $$= (64/27) – (32/9)$$ $$= (64/27) – (96/27) = -32/27$$

إذن:

$$\text{المسافة في الفترة الثانية} = 9 + 32/27 = 10.185$$

4. حساب المسافة الكلية

$$\text{المسافة الكلية} = 1.185 + 10.185 = 11.37$$

5. النتيجة النهائية

$$\boxed{11.37}$$

وهذا يعني أن الجسم قطع مسافة إجمالية مقدارها 11.37 وحدة خلال الفترة الزمنية $[0, 3]$.

الملخص العام للحل

1. حللنا دالة السرعة لإيجاد نقاط التوقف.
2. قسمنا التكامل إلى فترتين حيث السرعة سالبة أو موجبة.
3. أجرينا التكامل في كل فترة باستخدام القيمة المطلقة عندما تكون السرعة سالبة.
4. جمعنا النتائج للحصول على المسافة الكلية المقطوعة.

ملاحظات تطبيقية

• هذا النوع من التطبيقات يستخدم في الكينماتيكا الميكانيكية (Kinematics) لتحليل حركة الأجسام.
• يستخدم التكامل بشكل عام في حسابات مثل المسافة المقطوعة، الشغل المبذول، كمية السائل المتدفقة، والشحنات الكهربائية المتراكمة.

الرسم البياني للسرعة وحساب المسافة بالتكامل

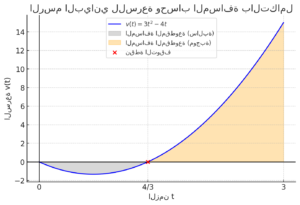
هذا هو الرسم البياني لدالة السرعة $v(t) = 3t^2 – 4t$.

• المنطقة المظللة باللون الرمادي تمثل الجزء حيث السرعة سالبة، وتم احتساب المسافة فيه بأخذ القيمة المطلقة.
• المنطقة المظللة باللون البرتقالي تمثل الجزء حيث السرعة موجبة، وتكاملها يعطينا المسافة مباشرة.
• النقطة الحمراء عند $t = 4/3$ هي نقطة التوقف، حيث تتغير إشارة السرعة.

هذا يوضح كيف يتم حساب المسافة باستخدام التكامل مع الأخذ في الاعتبار القيم المطلقة في المناطق التي تتغير فيها السرعة.