المعادلات التفاضلية / المحاضرة الاولى

شرح المعادلات التفاضلية

1. تعريف المعادلات التفاضلية

المعادلة التفاضلية هي معادلة تحتوي على مشتقات دالة غير معروفة بالنسبة لمتغير مستقل واحد أو أكثر. تُستخدم هذه المعادلات في نمذجة العديد من الظواهر الفيزيائية والهندسية والبيولوجية.

2. أنواع المعادلات التفاضلية

يمكن تصنيف المعادلات التفاضلية إلى عدة أنواع رئيسية:

1. حسب نوع المشتقات:
   • المعادلات التفاضلية العادية (ODE – Ordinary Differential Equations): تحتوي على مشتقات بالنسبة لمتغير مستقل واحد فقط.
   • المعادلات التفاضلية الجزئية (PDE – Partial Differential Equations): تحتوي على مشتقات جزئية بالنسبة لأكثر من متغير مستقل.
2. حسب الدرجة:
   • المعادلة التفاضلية من الدرجة الأولى: تحتوي على أعلى مشتقة من الدرجة الأولى فقط.
   • المعادلة التفاضلية من الدرجة الثانية: تحتوي على مشتقات حتى الدرجة الثانية، وهكذا.
3. حسب الترتيب:
   • يُحدد الترتيب بأعلى مشتقة موجودة في المعادلة. على سبيل المثال، المعادلة:
     $$\frac{d^2y}{dx^2} + 3\frac{dy}{dx} + 2y = 0$$ 

     هي معادلة تفاضلية من الدرجة الثانية والترتيب الثاني.

4. حسب الخطية:
   • المعادلات التفاضلية الخطية: تكون جميع الحدود التي تحتوي على الدالة والمتغيرات مشتقاتها خطية.
   • المعادلات التفاضلية غير الخطية: تحتوي على حدود غير خطية، مثل وجود الدالة مضروبة في مشتقاتها.

3. طرق حل المعادلات التفاضلية

هناك العديد من الطرق لحل المعادلات التفاضلية، ومن أهمها:

1. الفصل بين المتغيرات (Separation of Variables):
   • تُستخدم إذا كان من الممكن كتابة المعادلة على الشكل:
     $$f(y) \, dy = g(x) \, dx$$ 
   • ثم يتم التكامل على الطرفين.
2. العامل التكامل (Integrating Factor):
   • تُستخدم لحل المعادلات الخطية من الدرجة الأولى التي تكون على الشكل:
     $$\frac{dy}{dx} + P(x)y = Q(x)$$ 
   • يتم ضرب المعادلة بعامل تكامل مناسب.
3. طريقة التكامل المباشر:
   • تُستخدم عندما يمكن إيجاد الحل من خلال التكامل المباشر لبعض المشتقات.
4. طريقة تحويل لابلاس (Laplace Transform):
   • تُستخدم لتحويل المعادلات التفاضلية إلى معادلات جبرية يمكن حلها بسهولة.
5. طريقة المعاملات المحددة (Method of Undetermined Coefficients):
   • تُستخدم لحل المعادلات الخطية غير المتجانسة ذات المعاملات الثابتة.
6. طريقة فروبنيوس (Frobenius Method):
   • تُستخدم لحل المعادلات التفاضلية حول نقاط شاذة.

4. تطبيقات المعادلات التفاضلية

المعادلات التفاضلية لها تطبيقات واسعة في العديد من المجالات، مثل:

• الفيزياء: دراسة حركة الأجسام، الدوائر الكهربائية، ميكانيكا الكم.
• الهندسة: تحليل الإجهاد والاهتزازات، تصميم الأنظمة الكهربائية والميكانيكية.
• الاقتصاد: نمذجة التغيرات في الأسواق المالية والنمو السكاني.
• البيولوجيا: دراسة انتشار الأمراض والنماذج السكانية.

5. مثال عملي لحل معادلة تفاضلية

المعادلة:

$$\frac{dy}{dx} = 3y$$

الحل باستخدام الفصل بين المتغيرات:

1. إعادة كتابة المعادلة:
   $$\frac{dy}{y} = 3dx$$ 
2. التكامل للطرفين:
   $$\int \frac{dy}{y} = \int 3dx$$ 

   $$\ln |y| = 3x + C$$ 

3. إيجاد الحل العام:
   $$y = Ce^{3x}$$ 

حيث

$C$

هو ثابت التكامل.

الرسم البياني للتفاضل

التفاضل يعبر عن معدل التغير اللحظي للدالة، أي ميل المماس لمنحنى الدالة في أي نقطة. يمكن تمثيل التفاضل بيانيًا باستخدام المشتقة الأولى أو الثانية لدالة معينة.

1. مفهوم التفاضل بيانيًا

• المشتقة الأولى
  $f'(x)$ 

  تمثل ميل المماس لمنحنى الدالة عند أي نقطة.

• إذا كانت
  $f'(x) > 0$ 

  ، فهذا يعني أن الدالة متزايدة عند تلك النقطة.

• إذا كانت
  $f'(x) < 0$ 

  ، فهذا يعني أن الدالة متناقصة عند تلك النقطة.

• النقاط حيث
  $f'(x) = 0$ 

  قد تشير إلى قيم قصوى محلية أو نقاط انقلاب.

• المشتقة الثانية
  $f”(x)$ 

  تحدد التقعر:

  • إذا كانت
    $f”(x) > 0$ 

    ، فالمنحنى مقعر لأعلى.

  • إذا كانت
    $f”(x) < 0$ 

    ، فالمنحنى مقعر لأسفل.

2. رسم بياني لتوضيح مفهوم التفاضل

سنقوم الآن برسم منحنى لدالة معينة مع توضيح المشتقة الأولى والثانية عليها.

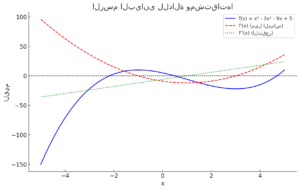
في الرسم البياني أعلاه:

• المنحنى الأزرق يمثل الدالة الأصلية
  $f(x) = x^3 – 3x^2 – 9x + 5$ 

  .

• المنحنى الأحمر المتقطع يمثل المشتقة الأولى
  $f'(x)$ 

  والتي تحدد ميل المماس عند كل نقطة.

• المنحنى الأخضر المنقط يمثل المشتقة الثانية
  $f”(x)$ 

  والتي تحدد التقعر (مقعر لأعلى أو لأسفل).

يمكنك ملاحظة أن:

• نقاط تقاطع المشتقة الأولى مع المحور
  $x$ 

  تعطي قيم قصوى محلية (نقاط حرجة).

• نقاط تقاطع المشتقة الثانية مع المحور
  $x$ 

  تعطي نقاط الانقلاب حيث يتغير التقعر.

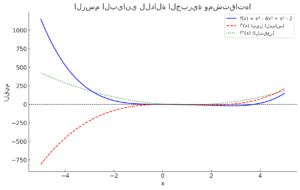
في هذا المثال، لدينا دالة جبرية:

$$f(x) = x^4 – 4x^3 + x^2 – 2$$

تحليل الرسم البياني:

• المنحنى الأزرق يمثل الدالة الأصلية.
• المنحنى الأحمر المتقطع يمثل المشتقة الأولى
  $f'(x)$ 

  ، والتي تحدد الميل.

• المنحنى الأخضر المنقط يمثل المشتقة الثانية
  $f”(x)$ 

  ، والتي تحدد التقعر.

الملاحظات:

1. نقاط حرجة: حيث
   $f'(x) = 0$ 

   ، وهذه قد تكون قيم قصوى محلية أو نقاط انقلاب.

2. التقعر: حيث
   $f”(x) = 0$ 

   ، يشير إلى تغير اتجاه التقعر.

هل لديك أي طلبات إضافية حول التحليل البياني أو نوع معين من الدوال؟ 😊