المحاضرة 22/ القطع الزائد / المقدمة

القطع الزائد: تعريفه، خواصه، وخطوات حل المسائل

تعريف القطع الزائد

القطع الزائد هو مجموعة من النقاط في المستوى بحيث يكون الفرق المطلق بين بعدي كل نقطة عن بؤرتين ثابتًا. ويشبه في شكله قطعتين متقابلتين مفتوحتين للخارج.

معادلة القطع الزائد

تأخذ معادلة القطع الزائد في المستوى الإحداثي الصيغتين التاليتين:

1. إذا كان المحور الأساسي أفقيًا:

   $$\frac{(x-h)^2}{a^2} – \frac{(y-k)^2}{b^2} = 1$$

   • مركز القطع: $(h, k)$
   • البؤرتان: $(h \pm c, k)$ حيث $c^2 = a^2 + b^2$
   • الرأسان: $(h \pm a, k)$
   • الخطان التقاربيان: $y – k = \pm \frac{b}{a} (x – h)$
2. إذا كان المحور الأساسي عموديًا:

   $$\frac{(y-k)^2}{a^2} – \frac{(x-h)^2}{b^2} = 1$$

   • مركز القطع: $(h, k)$
   • البؤرتان: $(h, k \pm c)$ حيث $c^2 = a^2 + b^2$
   • الرأسان: $(h, k \pm a)$
   • الخطان التقاربيان: $y – k = \pm \frac{a}{b} (x – h)$

خواص القطع الزائد

1. البؤرتان (Foci): المسافة بينهما تساوي $2c$ وتوجد على امتداد المحور الأساسي.
2. الرأسان (Vertices): يحددان امتداد الفرعين المفتوحين للقطع الزائد.
3. المركز (Center): نقطة المنتصف بين البؤرتين.
4. المحور الأساسي (Transverse Axis): المحور الذي يحتوي على الرؤوس والبؤرتين.
5. المحور المرافق (Conjugate Axis): المحور العمودي على المحور الأساسي.
6. الخطوط التقاربية (Asymptotes): خطوط تحدد اتجاه فرعي القطع الزائد ولكن لا تقطعه.

خطوات حل مسائل القطع الزائد

الخطوة 1: تحديد المعادلة القياسية

• إذا كانت المعادلة على شكل $Ax^2 + By^2 + Cx + Dy + E = 0$، يتم ترتيبها في الصورة القياسية بإكمال المربع.

الخطوة 2: تحديد المركز والبؤرتين والرؤوس

• يتم تحديد $h, k$ كمركز للقطع.
• حساب $a, b, c$ باستخدام العلاقة $c^2 = a^2 + b^2$.

الخطوة 3: رسم القطع الزائد

• تحديد المركز والرؤوس والبؤرتين.
• رسم المستطيل التوجيهي لتحديد اتجاه الخطين التقاربيين.
• رسم الخطين التقاربيين باستخدام معادلاتهما.

الخطوة 4: حل المسائل المتعلقة بالمواضع الهندسية

• إيجاد معادلة الخطوط التقاربية.
• إيجاد نقاط تقاطع القطع الزائد مع محاور الإحداثيات إذا لزم.
• إيجاد المسافة بين البؤرتين والرؤوس وغيرها من القيم المطلوبة.

أمثلة محلولة

مثال 1

أوجد معادلة القطع الزائد الذي مركزه $(0,0)$ وله بؤرتان عند $(\pm 5,0)$ ورأسان عند $(\pm 3,0)$.

الحل:

• المركز: $(0,0)$
• الرؤوس: $(\pm 3,0)$ أي $a = 3$
• البؤرتان: $(\pm 5,0)$ أي $c = 5$
• إيجاد $b^2$ من العلاقة $c^2 = a^2 + b^2$: $$5^2 = 3^2 + b^2$$ $$25 = 9 + b^2$$ $$b^2 = 16 \Rightarrow b = 4$$
• معادلة القطع الزائد: $$\frac{x^2}{3^2} – \frac{y^2}{4^2} = 1$$ أي: $$\frac{x^2}{9} – \frac{y^2}{16} = 1$$

مثال 2

أوجد معادلة الخطين التقاربيين للقطع الزائد في المثال السابق.

معادلة الخطوط التقاربية للقطع الزائد الأفقي:

$$y = \pm \frac{b}{a} x$$ $$y = \pm \frac{4}{3} x$$

ملخص سريع

1. حدد نوع القطع الزائد (أفقي أو عمودي).
2. استخرج القيم الأساسية $a, b, c$.
3. حدد المركز، البؤرتين، والرؤوس.
4. ارسم المستطيل التوجيهي والخطوط التقاربية.
5. استخدم المعادلات لحل أي مسائل إضافية.

بهذا يمكنك التعامل مع أي مسألة متعلقة بالقطع الزائد بسهولة! 🚀

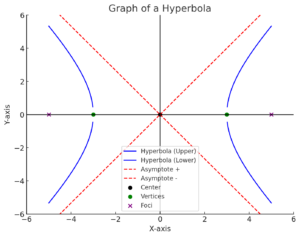
هذا هو الرسم البياني للقطع الزائد حيث تمثل الخطوط الزرقاء فروع القطع الزائد، والخطوط الحمراء المتقطعة تمثل الخطوط التقاربية. النقطة السوداء هي المركز، والنقاط الخضراء هي الرؤوس، بينما النقاط البنفسجية تمثل البؤرتين. إذا كنت بحاجة إلى تعديل القيم أو رسم نوع آخر من القطع الزائد، أخبرني بذلك! 😊