المجاميع العليا والسفلى/ الجزء الأول

في رياضيات الصف السادس العلمي، ترتبط المجاميع العليا والسفلى بمفهوم التكامل المحدود، حيث يتم استخدام مجاميع داربو العليا والسفلى (Darboux Upper and Lower Sums) لتقدير قيمة التكامل. هذا المفهوم يُعدّ الأساس لفهم التكامل كحد لمجاميع جزئية.

1. المجاميع العليا والسفلى في التكامل

عند دراسة التكامل المحدود لدالة $f(x)$ على الفترة $[a, b]$، يتم تقسيم هذه الفترة إلى أجزاء صغيرة، ثم يتم حساب القيم العظمى والصغرى للدالة داخل كل جزء. تُستخدم هذه القيم لحساب المجموع العلوي والمجموع السفلي اللذين يقتربان من التكامل الحقيقي.

أ) المجموع السفلي (Lower Sum)

المجموع السفلي يُمثِّل مجموع المساحات المستطيلة التي يتم تكوينها باستخدام أصغر قيمة للدالة داخل كل جزء من التقسيم.

يُحسب باستخدام الصيغة:

$$L(P) = \sum_{i=1}^{n} m_i \Delta x_i$$

حيث:

• $m_i = \min f(x)$ في كل جزء فرعي $[x_{i-1}, x_i]$ (أي أصغر قيمة للدالة داخل هذا الجزء).
• $\Delta x_i = x_i – x_{i-1}$ هو عرض الجزء الفرعي.

ب) المجموع العلوي (Upper Sum)

المجموع العلوي يُمثِّل مجموع المساحات المستطيلة التي يتم تكوينها باستخدام أكبر قيمة للدالة داخل كل جزء من التقسيم.

يُحسب باستخدام الصيغة:

$$U(P) = \sum_{i=1}^{n} M_i \Delta x_i$$

حيث:

• $M_i = \max f(x)$ في كل جزء فرعي $[x_{i-1}, x_i]$ (أي أكبر قيمة للدالة داخل هذا الجزء).
• $\Delta x_i$ هو عرض الجزء الفرعي.

2. تفسير رياضي للمجاميع العليا والسفلى

• كلما زاد عدد التقسيمات $n$ (أي أن عرض الأجزاء $\Delta x$ يصبح أصغر)، يقترب كل من المجموع العلوي والسفلي من قيمة التكامل الحقيقي.
• إذا كانت الدالة متصلة على الفترة $[a, b]$، فإن التكامل الحقيقي يساوي الحد المشترك للمجاميع العليا والسفلى عند $n \to \infty$: $$\lim_{n \to \infty} U(P) = \lim_{n \to \infty} L(P) = \int_a^b f(x) dx$$
• إذا كانت الدالة غير متصلة فقد لا يتطابق الحدّان، مما يعني أن التكامل غير معرف بطريقة داربو.

3. مثال توضيحي

لنفترض أننا نريد حساب التكامل التقريبي للدالة $f(x) = x^2$ على الفترة $[0, 2]$ باستخدام تقسيم بسيط إلى جزئين $[0,1]$ و $[1,2]$:

حساب المجموع السفلي:

• في الفترة $[0,1]$، القيم الدنيا: $m_1 = 0^2 = 0$
• في الفترة $[1,2]$، القيم الدنيا: $m_2 = 1^2 = 1$
• إذن: $$L(P) = (0 \times 1) + (1 \times 1) = 1$$

حساب المجموع العلوي:

• في الفترة $[0,1]$، القيم العظمى: $M_1 = 1^2 = 1$
• في الفترة $[1,2]$، القيم العظمى: $M_2 = 2^2 = 4$
• إذن: $$U(P) = (1 \times 1) + (4 \times 1) = 5$$

مع زيادة عدد التقسيمات، يقترب كلاهما من التكامل الحقيقي:

$$\int_0^2 x^2 dx = \frac{2^3}{3} – \frac{0^3}{3} = \frac{8}{3}$$

4. التطبيقات العملية للمجاميع العليا والسفلى في التكامل

• تستخدم لتقدير المساحات تحت المنحنيات في الفيزياء والهندسة.
• تُطبق في الاقتصاد والإحصاء لحساب المجاميع التراكمية.
• تُستخدم في تحليل البيانات لتحديد القيم التقريبية للأدلة الرياضية.

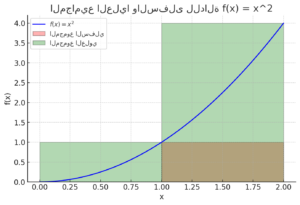
هذا هو الرسم البياني الذي يوضح المجاميع العليا والسفلى للدالة $f(x) = x^2$ على الفترة $[0,2]$.

• الخط الأزرق يمثل منحنى الدالة $x^2$.
• المستطيلات الحمراء تمثل المجموع السفلي (Lower Sum)، حيث يتم أخذ القيم الدنيا لكل جزء.
• المستطيلات الخضراء تمثل المجموع العلوي (Upper Sum)، حيث يتم أخذ القيم العظمى لكل جزء.

كلما زاد عدد التقسيمات، اقتربت قيمة هذه المجاميع من التكامل الحقيقي. 😊