المحاضرة 29 / تعريف القطع الزائد
إيجاد معادلة القطع الزائد باستخدام (التعريف)
إيجاد معادلة القطع الزائد باستخدام التعريف
1- تعريف القطع الزائد
القطع الزائد هو المجموعة الهندسية لجميع النقاط في المستوى بحيث يكون الفرق المطلق بين المسافتين من كل نقطة إلى بؤرتين ثابتًا.
2- معادلة القطع الزائد في المستوى الإحداثي
تنقسم معادلة القطع الزائد إلى نوعين، وذلك حسب موقع محوره الرئيسي:
- قطع زائد أفقي (محوره الرئيسي أفقي):
- قطع زائد رأسي (محوره الرئيسي رأسي):
حيث:
- (h, k): مركز القطع الزائد.
- a: المسافة من المركز إلى رأس القطع الزائد.
- b: تُحسب باستخدام العلاقة ، حيث هي المسافة من المركز إلى إحدى البؤرتين.
3- رسم بياني للقطع الزائد
سأقوم الآن بإنشاء رسم بياني يوضح شكل القطع الزائد الأفقي والرأسي.
هذا هو الرسم البياني للقطع الزائد الأفقي. في الرسم:
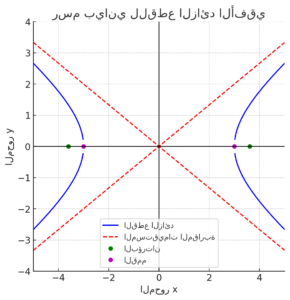
- المنحنى الأزرق يمثل القطع الزائد.
- الخطوط الحمراء المتقطعة هي المستقيمات المقاربة.
- النقاط الخضراء تمثل البؤرتين.
- النقاط البنفسجية تمثل القمم.
يمكنك ملاحظة أن القطع الزائد يقترب من المستقيمات المقاربة دون أن يلامسها.
السؤال:
باستخدام التعريف، جد معادلة القطع الزائد الذي بؤرتاه والقيمة المطلقة لفرق بعدي أي نقطة عنه البؤرتين يساوي وحدات.
لحل هذا السؤال، نستخدم تعريف القطع الزائد، والذي ينص على أن:
القطع الزائد هو مجموعة النقاط التي يكون الفرق المطلق بين بعديها عن بؤرتين ثابتًا.
1. استخراج المعطيات:
- إحداثيات البؤرتين: ، أي أن البؤرتين على المحور الأفقي.
- القيمة المطلقة لفرق بعدي أي نقطة عن البؤرتين = ، وبالتالي:
- المسافة بين البؤرتين:
إذن:
2. حساب :
العلاقة بين في القطع الزائد هي:
بالتعويض:
3. معادلة القطع الزائد:
بما أن القطع الزائد أفقي (لأن البؤرتين على المحور )، فإن معادلته تكون على الشكل:
بالتعويض بالقيم التي وجدناها:
إجابة نهائية:
معادلة القطع الزائد هي:
