التكامل – ايجاد المساحة بين منحني الدالة و محور السينات للدوال المثلثية / محاضرة 30

التكامل – إيجاد المساحة بين منحنى الدالة ومحور السينات للدوال المثلثية

إيجاد المساحة بين منحنيات الدوال المثلثية ومحور السينات يعتمد على التكامل المحدد. تُستخدم الدوال المثلثية مثل جيب الزاوية (sin) وجيب التمام (cos) وظل الزاوية (tan) لحساب المساحات تحت هذه المنحنيات.

1. القاعدة الأساسية لإيجاد المساحة

إذا كانت الدالة المثلثية $f(x)$ معرفة على الفترة $[a, b]$، فإن المساحة المحصورة بين منحنى الدالة ومحور السينات تُحسب بالتكامل المحدد:

$$A = \int_{a}^{b} |f(x)| \, dx$$

حيث:

• $a, b$ هما حدود التكامل.
• $f(x)$ هي الدالة المثلثية المعطاة.
• القيمة المطلقة $|f(x)|$ تُستخدم عند الحاجة إذا كانت الدالة سالبة في بعض الأجزاء.

2. حالات شائعة للدوال المثلثية

أ. المساحة تحت منحنى $y = \sin(x)$

$$A = \int_{a}^{b} \sin(x) \, dx = -\cos(x) \Big|_a^b$$

مثال: حساب المساحة تحت منحنى $y = \sin(x)$ في الفترة $[0, \pi]$:

$$A = -\cos(x) \Big|_0^\pi$$ $$= -\cos(\pi) + \cos(0) = -(-1) + 1 = 2$$

إذا كانت الفترة تشمل أجزاء حيث يكون الجيب سالبًا (مثلاً من $0$ إلى $2\pi$)، نقسم التكامل إلى جزأين ونجمع القيم المطلقة.

ب. المساحة تحت منحنى $y = \cos(x)$

$$A = \int_{a}^{b} \cos(x) \, dx = \sin(x) \Big|_a^b$$

مثال: حساب المساحة تحت منحنى $y = \cos(x)$ في الفترة $[0, \pi]$:

$$A = \sin(x) \Big|_0^\pi$$ $$= \sin(\pi) – \sin(0) = 0 – 0 = 0$$

في هذه الحالة، لا توجد مساحة لأن التكامل يعطي صفرًا، لكن إذا كان المطلوب المساحة المطلقة، نأخذ القيم الموجبة.

ج. المساحة تحت منحنى $y = \tan(x)$

التكامل الأساسي:

$$A = \int_{a}^{b} \tan(x) \, dx = \ln|\sec(x)| \Big|_a^b$$

يجب الانتباه إلى نقاط عدم التعريف عند $x = \frac{\pi}{2}, \frac{3\pi}{2}, \dots$.

3. أمثلة محلولة

مثال 1: حساب المساحة بين منحنى $y = \sin(x)$ ومحور السينات في الفترة $[0, 2\pi]$

نقسم التكامل إلى جزأين:

1. من $0$ إلى $\pi$ حيث $\sin(x)$ موجب
2. من $\pi$ إلى $2\pi$ حيث $\sin(x)$ سالب (نأخذ القيمة المطلقة)

$$A = \int_0^\pi \sin(x) \, dx + \left| \int_\pi^{2\pi} \sin(x) \, dx \right|$$ $$A = [-\cos(x)]_0^\pi + \left| [-\cos(x)]_\pi^{2\pi} \right|$$ $$A = [-(-1) + 1] + |[-1 – 1]|$$ $$A = [2] + | -2 |$$ $$A = 2 + 2 = 4$$

مثال 2: حساب المساحة بين منحنى $y = \cos(x)$ ومحور السينات في الفترة $[0, 2\pi]$

بما أن $\cos(x)$ يتغير من موجب إلى سالب عند $x = \pi$، نقسم التكامل إلى جزأين:

$$A = \int_0^\pi \cos(x) \, dx + \left| \int_\pi^{2\pi} \cos(x) \, dx \right|$$ $$A = [\sin(x)]_0^\pi + \left| [\sin(x)]_\pi^{2\pi} \right|$$ $$A = [0 – 0] + | [0 – 0] |$$ $$A = 0$$

أي أن المساحة تساوي 0، لأن التكامل على فترة متماثلة يلغى بعضه البعض.

4. استنتاجات هامة

• عند التعامل مع الدوال المثلثية، يجب الانتباه إلى الفترات التي تكون فيها الدالة موجبة وسالبة.
• إذا كان التكامل يعطي قيمة سالبة، فهذا يعني أن الجزء تحت المحور السينات، لذا نأخذ القيمة المطلقة.
• الدوال المثلثية دورية، لذا يمكن حساب المساحات المتكررة بسهولة باستخدام التناظر.

5. رسم بياني للتوضيح

سنقوم الآن برسم منحنى دالة جيب الزاوية $y = \sin(x)$ مع تظليل المساحة المطلوبة بين $x = 0$ و $x = 2\pi$.

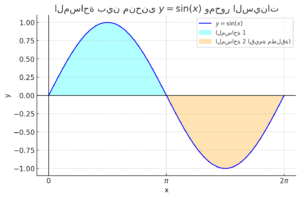
هذا الرسم البياني يوضح منحنى الدالة $y = \sin(x)$ مع تظليل المساحات الواقعة بين المنحنى ومحور السينات في الفترة $[0, 2\pi]$:

• المساحة المظللة باللون الأزرق الفاتح هي الجزء الموجب بين $x = 0$ و $x = \pi$.
• المساحة المظللة باللون البرتقالي هي الجزء السالب بين $x = \pi$ و $x = 2\pi$ (ونأخذ قيمته المطلقة عند حساب المساحة الكلية).

المساحة الكلية تساوي 4 وحدات مربعة. 🚀

السؤال المهم هو:

جد المساحة بين منحنى الدالة $y = 2\cos^2 x – 1$ ومحور السينات، وكان الفترة $[0, \frac{\pi}{2}]$.

لحساب المساحة المحصورة بين منحنى الدالة $y = 2\cos^2 x – 1$ ومحور السينات في الفترة $[0, \frac{\pi}{2}]$، نتبع الخطوات التالية:

1- تحديد نقاط التقاطع مع محور السينات:

نحدد القيم التي تجعل $y = 0$:

$$2\cos^2 x – 1 = 0$$ $$2\cos^2 x = 1$$ $$\cos^2 x = \frac{1}{2}$$ $$\cos x = \pm\frac{1}{\sqrt{2}}$$ $$x = \frac{\pi}{4}$$

إذن، يتقاطع المنحنى مع محور السينات عند $x = \frac{\pi}{4}$.

2- تقسيم التكامل:

بما أن الدالة تتغير إشارتها عند $x = \frac{\pi}{4}$، نقسم التكامل إلى جزأين:

• من $0$ إلى $\frac{\pi}{4}$ حيث $y$ موجب.
• من $\frac{\pi}{4}$ إلى $\frac{\pi}{2}$ حيث $y$ سالب.

لحساب المساحة نأخذ القيم المطلقة.

$$A = \int_0^{\frac{\pi}{4}} (2\cos^2 x – 1) \,dx – \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} (2\cos^2 x – 1) \,dx$$

3- حساب التكامل:

نستخدم متطابقة:

$$\cos^2 x = \frac{1 + \cos 2x}{2}$$

بالتالي:

$$2\cos^2 x – 1 = 2 \times \frac{1 + \cos 2x}{2} – 1 = 1 + \cos 2x – 1 = \cos 2x$$

إذن، التكامل يصبح:

$$A = \int_0^{\frac{\pi}{4}} \cos 2x \,dx – \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos 2x \,dx$$

نعرف أن:

$$\int \cos 2x \,dx = \frac{\sin 2x}{2}$$

نحسب التكامل الأول:

$$\left[ \frac{\sin 2x}{2} \right]_0^{\frac{\pi}{4}}$$ $$= \frac{\sin(\frac{\pi}{2})}{2} – \frac{\sin 0}{2} = \frac{1}{2} – 0 = \frac{1}{2}$$

ثم التكامل الثاني:

$$\left[ \frac{\sin 2x}{2} \right]_{\frac{\pi}{4}}^{\frac{\pi}{2}}$$ $$= \frac{\sin \pi}{2} – \frac{\sin(\frac{\pi}{2})}{2} = 0 – \frac{1}{2} = -\frac{1}{2}$$

نأخذ القيمة المطلقة:

$$A = \frac{1}{2} + \frac{1}{2} = 1$$

النتيجة النهائية:

المساحة المحصورة بين منحنى الدالة $y = 2\cos^2 x – 1$ ومحور السينات في الفترة $[0, \frac{\pi}{2}]$ هي 1 وحدة مربعة.

الرسم البياني للسؤال

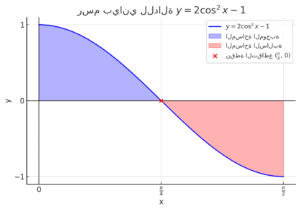
هذا هو الرسم البياني للدالة $y = 2\cos^2 x – 1$ في الفترة $[0, \frac{\pi}{2}]$:

• تمثل المنطقة المظللة باللون الأزرق المساحة التي تقع فوق محور السينات.
• تمثل المنطقة المظللة باللون الأحمر المساحة التي تقع تحت محور السينات (حيث القيم سالبة، لذلك نأخذ القيمة المطلقة عند حساب المساحة).
• النقطة الحمراء عند $x = \frac{\pi}{4}$ هي نقطة التقاطع بين المنحنى ومحور السينات.

المساحة الكلية المحصورة بين المنحنى ومحور السينات هي 1 وحدة مربعة.