تكامل الدالة الشطرية / محاضرة 22

تكامل الدالة الشطرية: شرح مفصل

1. ما هي الدالة الشطرية؟

الدالة الشطرية هي دالة تُعرف بأكثر من قاعدة في مجالات مختلفة من المتغير المستقل. أي أنها تُكتب على صورة:

$$f(x) = \begin{cases} f_1(x) , & a_1 \leq x < b_1 \\ f_2(x) , & a_2 \leq x < b_2 \\ \vdots \\ f_n(x) , & a_n \leq x < b_n \end{cases}$$

حيث كل جزء من الدالة $f_i(x)$ يتم تعريفه ضمن مجال معين.

2. كيفية حساب تكامل الدالة الشطرية؟

لحساب التكامل المحدد أو غير المحدد للدالة الشطرية، نقوم بتكامل كل جزء من الدالة ضمن مجاله المحدد.

(أ) التكامل غير المحدد:

يتم إيجاد التكامل غير المحدد لكل جزء من الدالة بشكل مستقل مع إضافة ثابت التكامل لكل منها.

(ب) التكامل المحدد:

لحساب التكامل المحدد للدالة الشطرية $f(x)$ على الفترة $[a, b]$، نقسم التكامل إلى تكاملات جزئية حسب المجالات المختلفة للدالة:

$$\int_{a}^{b} f(x) \,dx = \sum \int_{a_i}^{b_i} f_i(x) \,dx$$

حيث يتم حساب كل تكامل على حدة ثم يتم جمع القيم.

3. أمثلة على تكامل الدوال الشطرية

مثال 1: تكامل غير محدد

أوجد التكامل غير المحدد للدالة:

$$f(x) = \begin{cases} x^2, & x < 2 \\ 3x + 1, & x \geq 2 \end{cases}$$

الحل: نقوم بتكامل كل جزء على حدة:

1. لـ $x < 2$:

   $$\int x^2 \,dx = \frac{x^3}{3} + C_1$$

2. لـ $x \geq 2$:

   $$\int (3x + 1) \,dx = \frac{3x^2}{2} + x + C_2$$

إذن، التكامل غير المحدد هو:

$$F(x) = \begin{cases} \frac{x^3}{3} + C_1, & x < 2 \\ \frac{3x^2}{2} + x + C_2, & x \geq 2 \end{cases}$$

مثال 2: تكامل محدد

أوجد التكامل المحدد للدالة:

$$f(x) = \begin{cases} x, & 0 \leq x < 1 \\ 2, & 1 \leq x \leq 3 \end{cases}$$

على الفترة $[0,3]$.

الحل: نقسم التكامل إلى جزأين:

1. التكامل في الفترة $[0,1]$:

   $$\int_0^1 x \,dx = \frac{x^2}{2} \Big|_0^1 = \frac{1}{2} – 0 = \frac{1}{2}$$

2. التكامل في الفترة $[1,3]$:

   $$\int_1^3 2 \,dx = 2x \Big|_1^3 = 2(3) – 2(1) = 6 – 2 = 4$$

إذن، التكامل الكلي هو:

$$\frac{1}{2} + 4 = \frac{9}{2}$$

4. ملاحظات هامة عند تكامل الدالة الشطرية

• يجب تقسيم التكامل إلى تكاملات جزئية وفقًا لنطاقات تعريف كل جزء من الدالة.
• إذا كان هناك نقطة تغير في الدالة داخل فترة التكامل، يجب حساب التكامل قبل وبعد تلك النقطة بشكل منفصل.
• عند إيجاد التكامل غير المحدد، يتم استخدام ثوابت تكامل مختلفة لكل جزء.

خلاصة

• الدالة الشطرية تتكون من عدة أجزاء، لكل منها قاعدة خاصة بها.
• التكامل غير المحدد يتم لكل جزء على حدة مع ثوابت تكامل مستقلة.
• التكامل المحدد يتطلب تقسيم الفترة إلى أجزاء ومجموع ناتج التكاملات لكل جزء.
• يجب الانتباه إلى النقاط التي تتغير فيها قاعدة الدالة لتجنب الأخطاء.

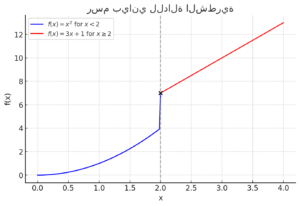
هذا هو الرسم البياني للدالة الشطرية التي تتغير عند $x = 2$.