تكامل الدالة المطلقة / محاضرة 23

تكامل الدالة المطلقة |𝑓(𝑥)|: شرح شامل مع أمثلة

1. ما هي الدالة المطلقة؟

الدالة المطلقة، التي تُرمز إليها بـ $|x|$، تُعرّف كالتالي:

$$|x| = \begin{cases} x, & \text{إذا كان } x \geq 0 \\ -x, & \text{إذا كان } x < 0 \end{cases}$$

2. كيفية تكامل الدالة المطلقة؟

بما أن الدالة المطلقة تُعرّف كدالة شطرية، فإن تكاملها يتطلب تقسيم التكامل إلى جزأين:

1. عندما يكون $x \geq 0$، فإن $|x| = x$.
2. عندما يكون $x < 0$، فإن $|x| = -x$.

3. حساب التكامل غير المحدد للدالة المطلقة

لحساب التكامل غير المحدد لـ $|x|$، نكامل كل شطر على حدة:

$$\int |x| \,dx = \begin{cases} \int x \,dx = \frac{x^2}{2} + C_1, & x \geq 0 \\ \int -x \,dx = -\frac{x^2}{2} + C_2, & x < 0 \end{cases}$$

4. حساب التكامل المحدد للدالة المطلقة

لحساب التكامل المحدد لـ $|x|$ على فترة معينة، نقسم التكامل عند النقطة التي يغيّر عندها $|x|$ تعريفه (عادةً عند $x = 0$).

مثال 1: تكامل محدد لـ $|x|$ على الفترة $[-3, 2]$

نحسب:

$$\int_{-3}^{2} |x| \,dx$$

الخطوة 1: تقسيم التكامل عند $x = 0$

$$\int_{-3}^{2} |x| \,dx = \int_{-3}^{0} -x \,dx + \int_{0}^{2} x \,dx$$

الخطوة 2: حساب التكاملات الجزئية

1. تكامل $-x$ على الفترة $[-3,0]$:

   $$\int -x \,dx = -\frac{x^2}{2}$$ $$\left[ -\frac{x^2}{2} \right]_{-3}^{0} = \left( -\frac{0^2}{2} \right) – \left( -\frac{(-3)^2}{2} \right) = 0 + \frac{9}{2} = \frac{9}{2}$$

2. تكامل $x$ على الفترة $[0,2]$:

   $$\int x \,dx = \frac{x^2}{2}$$ $$\left[ \frac{x^2}{2} \right]_{0}^{2} = \left( \frac{2^2}{2} \right) – \left( \frac{0^2}{2} \right) = \frac{4}{2} – 0 = 2$$

الخطوة 3: حساب المجموع النهائي

$$\frac{9}{2} + 2 = \frac{9}{2} + \frac{4}{2} = \frac{13}{2}$$

5. تعميم التكامل للدالة المطلقة

بشكل عام، إذا أردنا حساب التكامل المحدد للدالة المطلقة $|f(x)|$ في الفترة $[a,b]$، نقوم بالتالي:

1. نحدد القيم التي تجعل $f(x) = 0$ داخل الفترة (أي النقاط التي ينعكس عندها الاتجاه).
2. نقسم التكامل إلى أجزاء وفقًا لتغيّر تعريف الدالة المطلقة.
3. نحسب كل تكامل جزئي على حدة ونجمع النتائج.

6. رسم بياني للدالة المطلقة وتكاملها

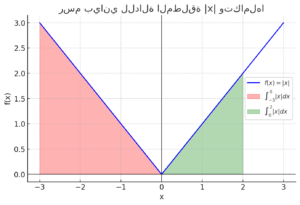
سأقوم الآن برسم الدالة المطلقة $|x|$ على الفترة $[-3,3]$ مع تمثيل المساحة تحت المنحنى (التكامل).

هذا هو الرسم البياني للدالة المطلقة $|x|$ مع تمثيل المساحة تحت المنحنى التي تمثل التكامل في الفترة $[-3,2]$. إذا كنت

السؤال:

احسب التكامل التالي:

$$I = \int_0^2 f(x) \, dx$$

حيث أن:

$$f(x) = |x – 1|$$

المسألة المعطاة تتطلب حساب التكامل التالي:

$$I = \int_0^2 f(x) \, dx$$

حيث أن:

$$f(x) = |x – 1|$$

الخطوة 1: تحليل القيمة المطلقة

الدالة

$f(x) = |x – 1|$

تتغير عند النقطة

$x = 1$

وبالتالي نحتاج إلى تقسيم التكامل إلى جزأين:

• عندما يكون
  $0 \leq x < 1$ 

  ، فإن $|x – 1| = 1 – x$ 

  .

• عندما يكون
  $1 \leq x \leq 2$ 

  ، فإن $|x – 1| = x – 1$ 

  .

الخطوة 2: تقسيم التكامل

نقسم التكامل إلى جزأين:

$$I = \int_0^1 (1 – x) \, dx + \int_1^2 (x – 1) \, dx$$

الخطوة 3: حساب كل تكامل على حدة

حساب التكامل الأول:

$$\int_0^1 (1 – x) \, dx = \int_0^1 1 \, dx – \int_0^1 x \, dx$$

نحسب كل جزء على حدة:

$$\int_0^1 1 \, dx = \left[ x \right]_0^1 = 1 – 0 = 1$$

$$\int_0^1 x \, dx = \left[ \frac{x^2}{2} \right]_0^1 = \frac{1}{2} – 0 = \frac{1}{2}$$

إذن:

$$\int_0^1 (1 – x) \, dx = 1 – \frac{1}{2} = \frac{1}{2}$$

حساب التكامل الثاني:

$$\int_1^2 (x – 1) \, dx = \int_1^2 x \, dx – \int_1^2 1 \, dx$$

نحسب كل جزء:

$$\int_1^2 x \, dx = \left[ \frac{x^2}{2} \right]_1^2 = \left( \frac{4}{2} – \frac{1}{2} \right) = 2 – \frac{1}{2} = \frac{4}{2} – \frac{1}{2} = \frac{3}{2}$$

$$\int_1^2 1 \, dx = \left[ x \right]_1^2 = 2 – 1 = 1$$

إذن:

$$\int_1^2 (x – 1) \, dx = \frac{3}{2} – 1 = \frac{1}{2}$$

الخطوة 4: إيجاد الناتج النهائي

بجمع القيمتين:

$$I = \frac{1}{2} + \frac{1}{2} = 1$$

النتيجة النهائية:

$$\int_0^2 |x – 1| \, dx = 1$$