الفصل الرابع / المراجعة المركزة ملخص الفصل الرابع التكامل

تلخيص لموضوع التكامل والمفاهيم الأساسية :

1. المجاميع العليا والسفلى:
   • تستخدم لتقدير مساحة المنطقة تحت المنحنى، وهي أساس تعريف التكامل المحدد.
   • المجاميع العليا تعتمد على القيم العليا للوظيفة في الفترات الجزئية، بينما المجاميع السفلى تعتمد على القيم الدنيا.
2. الدالة المقابلة:
   • تعبر عن العلاقة بين تكامل الدالة ومجالها، وتستخدم في تحديد الدوال الأصلية للتكاملات.
3. التكامل غير المحدد للدوال الجبرية والمثلثية:
   • هو عملية إيجاد الدالة الأصلية التي تشتق إلى الدالة المعطاة.
   • يتضمن قوانين التكامل الأساسية مثل تكامل القوى، الدوال المثلثية، والقواعد الأساسية للتكامل.
4. التكامل المحدد للدوال الجبرية والمثلثية:
   • هو حساب المساحة تحت منحنى الدالة بين حدين معينين.
   • يعتمد على مبرهنة القيمة الأساسية للتكامل.
5. خواص التكامل المحدد + إيجاد الثوابت:
   • تتضمن القواعد الأساسية مثل الخطية، الإضافية، والانعكاسية.
   • يستخدم في تحديد الثوابت عند إيجاد الدالة الأصلية.
6. تكامل الدوال الشطرية + الدوال المطلقة:
   • الدوال الشطرية هي الدوال التي تُعرف على أجزاء منفصلة من المجال، ويحتاج تكاملها إلى تحليل كل جزء على حدة.
   • تكامل الدوال المطلقة يتم بتحديد القيم التي تغير عندها الإشارة وتقسيم التكامل وفقًا لذلك.
7. تكامل الدوال اللوغاريتمية والأسية:
   • يشمل تكامل الدوال مثل $e^x$ و $\ln x$، والتي لها قواعد تكامل محددة.
   • التكامل بالدوال اللوغاريتمية يستخدم أحيانًا في التكامل بالتجزئة.
8. التطبيقات الهندسية للتكامل:
   • المساحة: حساب المساحة بين منحنيين باستخدام التكامل المحدد.
   • المسافة: حساب المسافة الكلية المقطوعة باستخدام التكامل للسرعة.
   • الحجوم: إيجاد حجوم الأجسام الدورانية باستخدام طرق التكامل مثل طريقة الأقراص والأسطوانات.

السؤال الاول:

“لتكن $F$ دالة معرفة على الفترة $[0,5]$ حيث:
$F(x) = 5 – 2x$
وإذا كانت $\Theta = \{0,1,3,5\}$، فجد كلاً من:

• المجموع الأعلى $U$ على الفترة $(0,5)$
• المجموع الأسفل $L$ على الفترة $(0,5)$“

الحل :

لحل هذا السؤال وإيجاد المجموع الأعلى $U$ و المجموع الأسفل $L$، نتبع الخطوات التالية:

1. فهم معنى المجاميع العليا والسفلى:

• المجموع الأعلى $U$ هو مجموع المساحات المستطيلة حيث يتم استخدام القيم العظمى للدالة في كل فترة جزئية.
• المجموع الأسفل $L$ هو مجموع المساحات المستطيلة حيث يتم استخدام القيم الدنيا للدالة في كل فترة جزئية.

2. تحديد الفواصل الجزئية:

المجموعة المعطاة:

$$\Theta = \{0,1,3,5\}$$

تعني أننا نقسم الفترة $[0,5]$ إلى الفترات الجزئية التالية:

• $[0,1]$
• $[1,3]$
• $[3,5]$

3. إيجاد القيم العظمى والصغرى للدالة في كل فترة جزئية:

الدالة المعطاة:

$$F(x) = 5 – 2x$$

وهي دالة خطية متناقصة لأن معامل $x$ سالب.
بالتالي، القيم العظمى والصغرى في كل فترة جزئية ستكون عند أطراف الفترات.

في الفاصل $[0,1]$:

• $F(0) = 5$ (القيمة العظمى)
• $F(1) = 3$ (القيمة الصغرى)

في الفاصل $[1,3]$:

• $F(1) = 3$ (القيمة العظمى)
• $F(3) = -1$ (القيمة الصغرى)

في الفاصل $[3,5]$:

• $F(3) = -1$ (القيمة العظمى)
• $F(5) = -5$ (القيمة الصغرى)

4. حساب المجاميع العليا والسفلى

حساب المجموع الأعلى $U$:

يتم استخدام القيمة العظمى لكل فترة:

$$U = (5 \times 1) + (3 \times 2) + (-1 \times 2)$$ $$U = 5 + 6 – 2 = 9$$

حساب المجموع الأسفل $L$:

يتم استخدام القيمة الصغرى لكل فترة:

$$L = (3 \times 1) + (-1 \times 2) + (-5 \times 2)$$ $$L = 3 – 2 – 10 = -9$$

5. النتيجة النهائية:

• المجموع الأعلى $U = 9$
• المجموع الأسفل $L = -9$

ملاحظات إضافية:

• بما أن الدالة متناقصة، يكون المجموع الأعلى دائمًا أكبر من المجموع الأسفل.
• لو أردنا تقريب التكامل المحدد للدالة باستخدام هذه المجاميع، يمكننا استخدام مفهوم حساب التكامل باستخدام مجموع ريمان.

السؤال الثاني:

“لتكن $F(x) = 2x + 5$ معرفة على الفترة $[0,4]$
وإذا كانت $\Theta = \{0,1,2,4\}$، فباستخدام التجزئة، جد المساحة تحت المنحنى.”

حل السؤال لإيجاد المساحة تحت المنحنى باستخدام التجزئة

1. فهم السؤال

نريد حساب المساحة تحت المنحنى للدالة:

$$F(x) = 2x + 5$$

ضمن الفترة $[0,4]$ باستخدام التجزئة المعطاة:

$$\Theta = \{0,1,2,4\}$$

هذه التجزئة تقسم الفترة إلى الفترات الجزئية التالية:

• $[0,1]$
• $[1,2]$
• $[2,4]$

2. حساب قيم الدالة عند نقاط التقسيم

نحسب قيم $F(x)$ عند النقاط في المجموعة $\Theta$:

$$F(0) = 2(0) + 5 = 5$$ $$F(1) = 2(1) + 5 = 7$$ $$F(2) = 2(2) + 5 = 9$$ $$F(4) = 2(4) + 5 = 13$$

3. استخدام طريقة التجزئة لحساب المساحة

المساحة تحت المنحنى تُحسب كمجموع المساحات للمستطيلات التي عرضها هو طول كل فترة جزئية، وارتفاعها يتم أخذه باستخدام قيمة الدالة عند الطرف الأيسر (طريقة المجموع السفلي) أو الطرف الأيمن (طريقة المجموع العلوي).

طريقة المجموع السفلي:

نستخدم القيم عند البدايات لكل فترة:

$$\text{المساحة} = \sum \text{(عرض الفاصل)} \times \text{(قيمة الدالة عند بداية الفاصل)}$$ $$= (1 \times F(0)) + (1 \times F(1)) + (2 \times F(2))$$ $$= (1 \times 5) + (1 \times 7) + (2 \times 9)$$ $$= 5 + 7 + 18 = 30$$

طريقة المجموع العلوي:

نستخدم القيم عند النهايات لكل فترة:

$$\text{المساحة} = (1 \times F(1)) + (1 \times F(2)) + (2 \times F(4))$$ $$= (1 \times 7) + (1 \times 9) + (2 \times 13)$$ $$= 7 + 9 + 26 = 42$$

4. النتيجة النهائية

المساحة المحصورة تحت المنحنى تقارب القيمتين المحسوبتين:

$$30 \leq \text{المساحة الفعلية} \leq 42$$

أي أن المساحة الحقيقية تقع بين 30 و 42، ويمكن حساب التكامل المحدد للحصول على القيمة الدقيقة.

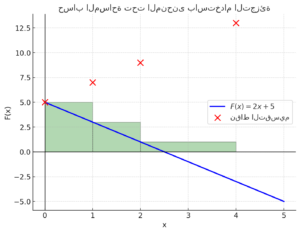
هذا هو الرسم البياني للدالة $F(x) = 2x + 5$ مع تمثيل المساحة تحت المنحنى باستخدام التجزئة:

• الخط الأزرق يمثل الدالة $F(x)$.
• النقاط الحمراء تمثل القيم عند نقاط التقسيم $\Theta = \{0,1,2,4\}$.
• المستطيلات الخضراء تمثل تقدير المساحة باستخدام المجاميع السفلى، حيث يتم استخدام قيم الدالة عند بدايات الفترات الجزئية.

يمكنك ملاحظة كيف يتم تقسيم المنطقة إلى مستطيلات لتقدير المساحة تحت المنحنى