الفصل الرابع / المراجعة التكامل – الدالة المقابلة
شرح مفهوم الدالة المقابلة
1. تعريف الدالة المقابلة
الدالة المقابلة (وتسمى أيضًا الدالة الأصلية أو المكاملة الأولية) لدالة معينة هي دالة إذا اشتُقّت فإنها تعيد الدالة الأصلية المعطاة. بعبارة أخرى، إذا كانت لدينا دالة ، فإن الدالة المقابلة لها تحقق العلاقة التالية:
بمعنى أن التكامل غير المحدد لدالة يعطينا الدالة الأصلية ، والتي تمثل “الدالة المقابلة” لها.
2. العلاقة بين الدالة المقابلة والتكامل
نظرًا لأن التكامل هو العملية العكسية للاشتقاق، فإن إيجاد الدالة المقابلة يكون عن طريق حساب التكامل غير المحدد:
ومن ثم، فإن اشتقاق سيعيدنا إلى :
وهذا يعبر عن فكرة أن التكامل والتفاضل عمليتان متعاكستان.
3. مثال على الدالة المقابلة
لنأخذ الدالة التالية:
لإيجاد الدالة المقابلة ، نحسب التكامل:
نستخدم قاعدة التكامل:
فنحصل على:
إذن، الدالة المقابلة لـ هي:
حيث هو ثابت التكامل، وهو ضروري لأنه يمكن أن يكون لأي دالة أصلية عدد غير محدد من الدوال المقابلة يختلف كل منها بثابت.
4. تفسير بياني للدالة المقابلة
إذا رسمنا منحنى ، فإن الدالة المقابلة تمثل المساحة المتراكمة تحت منحنى حتى النقطة . أي أن الدالة الأصلية تعبر عن الكمية المتراكمة التي تزداد كلما زاد .
5. تطبيقات الدالة المقابلة
- حساب المساحات تحت المنحنيات: تُستخدم الدالة المقابلة لحساب التكاملات المحددة، التي تعطي المساحة المحصورة بين منحنى الدالة والمحور السيني.
- الفيزياء والميكانيكا: في قوانين الحركة، الدالة المقابلة للسرعة تعطي الإزاحة، والدالة المقابلة للتسارع تعطي السرعة.
- الهندسة والاقتصاد: تُستخدم في حساب التغيرات الكلية في الكميات مثل النمو السكاني والتدفق النقدي والتغيرات في الطلب والعرض.
6. قاعدة عامة للدالة المقابلة
بشكل عام، إذا كانت ، فإن الدالة المقابلة هي:
وهذه القاعدة تسهل حساب التكاملات الأساسية لإيجاد الدوال المقابلة.
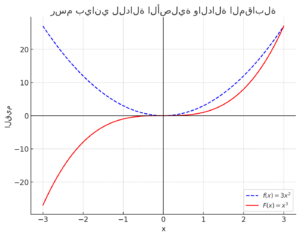
في الرسم البياني أعلاه:
- الخط الأزرق المتقطع يمثل الدالة الأصلية .
- الخط الأحمر المتصل يمثل الدالة المقابلة .
يوضح الرسم العلاقة بين الدالتين: الدالة المقابلة هي تكامل ، أي أن أي نقطة على منحنى تمثل المساحة المتراكمة تحت منحنى حتى تلك النقطة.
السؤال الاول
لإثبات أن الدالة مقابلة على المجال ، يجب علينا التحقق مما إذا كانت الدالة على (Surjective) على مدى معين، أو أنها متباينة (Injective)، مما يؤدي إلى كونها تقابلية (Bijective).
1- فحص الرتابة (التباين) باستخدام المشتقة:
لحساب المشتقة الأولى:
بما أن موجبة دائمًا لكل ، فإن الدالة رُتَبية تصاعدية (متزايدة تمامًا).
وهذا يعني أن لكل بحيث يكون .
إذن، الدالة واحد لواحد (Injective).
2- التحقق من أن الدالة تغطي مدى معين (Surjective)
نحسب قيم عند طرفي المجال:
- عند :
- عند :
إذن، مدى الدالة هو ، وهو مجموعة القيم التي تأخذها ضمن المجال المعطى.
3- الاستنتاج
بما أن متزايدة تمامًا، فهي متباينة (Injective)،
وبما أن مدى الدالة هو ، فإنها على (Surjective) على هذا المدى.
وبالتالي، الدالة مقابلة (Bijection) على المجال المعطى.
✅ الإجابة: الدالة مقابلة على المجال .
السؤال الرابع هو:
س 4 إذا كانت دالة مستمرة على الفترة حيث ، هل دالة مقابلة للدالة ؟
لحل السؤال، سنقوم بتحليل المعطيات والتحقق مما إذا كانت دالة مقابلة للدالة التكاملية المعطاة.
الخطوات:
1. حساب التكامل المحدد:
المطلوب حساب:
نعلم أن:
وبتطبيق حدود التكامل:
نحسب القيم عند الحدود:
حيث:
إذن:
السؤال الخامس
السؤال كما هو في الصورة:
س 5 اثبت أن الدالة هي دالة مقابلة، ثم أوجد
حيث:
لحل السؤال، سنتبع الخطوات التالية:
أولًا: إثبات أن دالة مقابلة
الدالة تكون مقابلة إذا كانت متباينة، أي أنها إما متزايدة تمامًا أو متناقصة تمامًا على المجال المحدد.
1. إيجاد المشتقة :
معطى أن:
نشتق:
2. فحص إشارة على المجال :
- نعلم أن الدالة تتذبذب بين القيم الموجبة والسالبة داخل الفترة ، أي أنها ليست دالة متزايدة تمامًا أو متناقصة تمامًا على هذا المجال.
- بما أن يغيّر إشارته، فإن ليست متباينة على المجال وبالتالي ليست مقابلة.
ثانيًا: إيجاد التكامل
1. حساب التكامل غير المحدد:
نعلم أن:
2. حساب التكامل المحدود:
نحسب القيم عند الحدود:
وبما أن:
إذن:
النتيجة النهائية:
- الدالة ليست مقابلة لأنها غير متباينة على الفترة .
- قيمة التكامل هي:
السؤال التاسع
نستخدم قاعدة تكامل القوى:
التطبيق:
هنا ، فنضيف 1 إلى الأس:
إذن:
تبسيط الكسر:
النتيجة النهائية:
السؤال العاشر
نستخدم قاعدة تكامل القوى:
التطبيق:
هنا ، فنضيف 1 إلى الأس:
إذن:
تبسيط الكسر:
النتيجة النهائية:
السؤال 11
الخطوة 1: تحويل الجذر إلى صورة أس
نعلم أن:
إذن يمكننا إعادة كتابة التكامل على الشكل:
الخطوة 2: استخدام قاعدة تكامل القوى
قاعدة التكامل هي:
هنا ، فنضيف 1 إلى الأس:
إذن:
الخطوة 3: تبسيط الكسر
النتيجة النهائية:
