VIDEO
مراجعة الفصل الرابع في التكامل و ايجاد المجهول في الاسئلة و التمارين
السؤال: رقم 1 (وزاري) أوجد قيمة b b
∫ 0 b 3 x x 2 + 16 d x = 61 \int_{0}^{b} 3x \sqrt{x^2 + 16} \, dx = 61
الحل: لحل التكامل:
I = ∫ 3 x x 2 + 16 d x I = \int 3x \sqrt{x^2 + 16} \, dx
نستخدم التعويض التالي:
u = x 2 + 16 ⇒ d u = 2 x d x u = x^2 + 16 \Rightarrow du = 2x dx
إذن:
d u 2 = x d x \frac{du}{2} = x dx
بالتعويض في التكامل:
I = ∫ 3 ⋅ d u 2 ⋅ u I = \int 3 \cdot \frac{du}{2} \cdot \sqrt{u} = 3 2 ∫ u d u = \frac{3}{2} \int \sqrt{u} \, du
نعرف أن:
∫ u 1 2 d u = 2 3 u 3 2 \int u^{\frac{1}{2}} \, du = \frac{2}{3} u^{\frac{3}{2}}
وبالتالي نحصل على:
I = 3 2 × 2 3 u 3 2 I = \frac{3}{2} \times \frac{2}{3} u^{\frac{3}{2}} = u 3 2 = ( x 2 + 16 ) 3 2 = u^{\frac{3}{2}} = (x^2 + 16)^{\frac{3}{2}}
إذن:
∫ 0 b 3 x x 2 + 16 d x = [ ( x 2 + 16 ) 3 2 ] 0 b \int_{0}^{b} 3x \sqrt{x^2 + 16} \, dx = \left[ (x^2 + 16)^{\frac{3}{2}} \right]_{0}^{b} = ( b 2 + 16 ) 3 2 − ( 0 2 + 16 ) 3 2 = (b^2 + 16)^{\frac{3}{2}} – (0^2 + 16)^{\frac{3}{2}} = ( b 2 + 16 ) 3 2 − 16 3 2 = (b^2 + 16)^{\frac{3}{2}} – 16^{\frac{3}{2}}
وبما أن:
16 3 2 = ( 4 2 ) 3 2 = 4 3 = 64 16^{\frac{3}{2}} = (4^2)^{\frac{3}{2}} = 4^3 = 64
فإن المعادلة تصبح:
( b 2 + 16 ) 3 2 − 64 = 61 (b^2 + 16)^{\frac{3}{2}} – 64 = 61 ( b 2 + 16 ) 3 2 = 125 (b^2 + 16)^{\frac{3}{2}} = 125 b 2 + 16 = 125 2 3 b^2 + 16 = 125^{\frac{2}{3}} b 2 + 16 = 125 2 3 = ( 5 3 ) 2 3 = 5 2 = 25 b^2 + 16 = 125^{\frac{2}{3}} = (5^3)^{\frac{2}{3}} = 5^2 = 25 b 2 = 25 − 16 b^2 = 25 – 16 b 2 = 9 b^2 = 9 b = ± 3 b = \pm 3
بما أن b ∈ R b \in \mathbb{R} b b b = 3 b = 3 b = − 3 b = -3
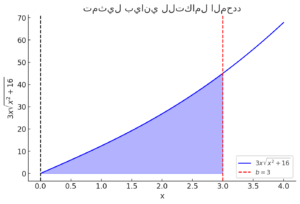
تمثيل بياني للتكامل المحدد هذا هو التمثيل البياني للتكامل المحدد ∫ 0 3 3 x x 2 + 16 d x \int_{0}^{3} 3x \sqrt{x^2 + 16} \, dx x = 0 x = 0 x = 3 x = 3 61 61 x = 3 x = 3 b b
السؤال: رقم 2 أوجد قيمتي a a b b
∫ a b ( 2 x + 3 ) d x = 12 \int_{a}^{b} (2x + 3) \, dx = 12
ومعطى أن:
a + 2 b = 3 a + 2b = 3
الحل: 1- حساب التكامل: نحسب التكامل غير المحدد:
∫ ( 2 x + 3 ) d x = x 2 + 3 x + C \int (2x + 3) \, dx = x^2 + 3x + C
إذن التكامل المحدد هو:
∫ a b ( 2 x + 3 ) d x = [ x 2 + 3 x ] a b \int_{a}^{b} (2x + 3) \, dx = \left[ x^2 + 3x \right]_{a}^{b} = ( b 2 + 3 b ) − ( a 2 + 3 a ) = (b^2 + 3b) – (a^2 + 3a)
وبالتعويض بالقيمة المعطاة:
( b 2 + 3 b ) − ( a 2 + 3 a ) = 12 (b^2 + 3b) – (a^2 + 3a) = 12
2- حل المعادلتين معًا: لدينا المعادلتين:
b 2 + 3 b − a 2 − 3 a = 12 b^2 + 3b – a^2 – 3a = 12 a + 2 b = 3 a + 2b = 3 a a
a = 3 − 2 b a = 3 – 2b
3- التعويض في معادلة التكامل: نستبدل a a
b 2 + 3 b − ( ( 3 − 2 b ) 2 + 3 ( 3 − 2 b ) ) = 12 b^2 + 3b – ( (3 – 2b)^2 + 3(3 – 2b) ) = 12
نحسب ( 3 − 2 b ) 2 (3 – 2b)^2
( 3 − 2 b ) 2 = 9 − 12 b + 4 b 2 (3 – 2b)^2 = 9 – 12b + 4b^2
ونحسب 3 ( 3 − 2 b ) 3(3 – 2b)
9 − 6 b 9 – 6b
إذن تصبح المعادلة:
b 2 + 3 b − ( 9 − 12 b + 4 b 2 + 9 − 6 b ) = 12 b^2 + 3b – (9 – 12b + 4b^2 + 9 – 6b) = 12 b 2 + 3 b − ( 18 − 18 b + 4 b 2 ) = 12 b^2 + 3b – (18 – 18b + 4b^2) = 12 b 2 + 3 b − 18 + 18 b − 4 b 2 = 12 b^2 + 3b – 18 + 18b – 4b^2 = 12 − 3 b 2 + 21 b − 18 = 12 -3b^2 + 21b – 18 = 12 − 3 b 2 + 21 b − 30 = 0 -3b^2 + 21b – 30 = 0
نقسم على -3:
b 2 − 7 b + 10 = 0 b^2 – 7b + 10 = 0
4- حل المعادلة التربيعية: نحلل المعادلة:
( b − 5 ) ( b − 2 ) = 0 (b – 5)(b – 2) = 0
إذن:
b = 5 أو b = 2 b = 5 \quad \text{أو} \quad b = 2
5- إيجاد قيم a a باستخدام a = 3 − 2 b a = 3 – 2b
a = 3 − 2 ( 5 ) = 3 − 10 = − 7 a = 3 – 2(5) = 3 – 10 = -7
a = 3 − 2 ( 2 ) = 3 − 4 = − 1 a = 3 – 2(2) = 3 – 4 = -1
الإجابة النهائية: الحلان الممكنان هما:
a = − 7 a = -7 b = 5 b = 5
a = − 1 a = -1 b = 2
السؤال: رقم3 (سؤال الكتاب) أوجد قيمة a a
∫ 1 a ( x + 1 2 ) d x = 2 ∫ 0 π 4 sec 2 x d x \int_{1}^{a} \left(x + \frac{1}{2}\right) dx = 2 \int_{0}^{\frac{\pi}{4}} \sec^2 x \, dx
مع العلم أن a ∈ R a \in \mathbb{R}
الحل: 1- حساب التكامل الأول: نحسب:
I 1 = ∫ ( x + 1 2 ) d x I_1 = \int (x + \frac{1}{2}) \, dx
نقوم بتجزئة التكامل:
I 1 = ∫ x d x + ∫ 1 2 d x I_1 = \int x \, dx + \int \frac{1}{2} \, dx = x 2 2 + x 2 + C = \frac{x^2}{2} + \frac{x}{2} + C
إذن التكامل المحدد:
∫ 1 a ( x + 1 2 ) d x = [ x 2 2 + x 2 ] 1 a \int_{1}^{a} \left(x + \frac{1}{2}\right) dx = \left[ \frac{x^2}{2} + \frac{x}{2} \right]_{1}^{a} = ( a 2 2 + a 2 ) − ( 1 2 2 + 1 2 ) = \left(\frac{a^2}{2} + \frac{a}{2}\right) – \left(\frac{1^2}{2} + \frac{1}{2}\right) = ( a 2 2 + a 2 ) − ( 1 2 + 1 2 ) = \left(\frac{a^2}{2} + \frac{a}{2}\right) – \left(\frac{1}{2} + \frac{1}{2}\right) = ( a 2 2 + a 2 ) − 1 = \left(\frac{a^2}{2} + \frac{a}{2}\right) – 1 = a 2 2 + a 2 − 1 = \frac{a^2}{2} + \frac{a}{2} – 1
2- حساب التكامل الثاني: نعلم أن:
∫ sec 2 x d x = tan x + C \int \sec^2 x \, dx = \tan x + C
إذن التكامل المحدد:
∫ 0 π 4 sec 2 x d x = [ tan x ] 0 π 4 \int_{0}^{\frac{\pi}{4}} \sec^2 x \, dx = \left[ \tan x \right]_{0}^{\frac{\pi}{4}} = tan π 4 − tan 0 = \tan \frac{\pi}{4} – \tan 0 = 1 − 0 = 1 = 1 – 0 = 1
وبما أن التكامل الثاني مضروب في 2:
2 × 1 = 2 2 \times 1 = 2
3- إيجاد قيمة a a من المعادلة:
a 2 2 + a 2 − 1 = 2 \frac{a^2}{2} + \frac{a}{2} – 1 = 2
نضرب الطرفين في 2 للتخلص من الكسر:
a 2 + a − 2 = 4 a^2 + a – 2 = 4 a 2 + a − 6 = 0 a^2 + a – 6 = 0
نحلل المعادلة التربيعية:
( a + 3 ) ( a − 2 ) = 0 (a + 3)(a – 2) = 0
إذن:
a + 3 = 0 ⇒ a = − 3 a + 3 = 0 \quad \Rightarrow \quad a = -3 a − 2 = 0 ⇒ a = 2 a – 2 = 0 \quad \Rightarrow \quad a = 2
الإجابة النهائية: a = 2 أو a = − 3 a = 2 \quad \text{أو} \quad a = -3
السؤال: الرقم 6 جد قيمة التكامل:
∫ 0 4 x ( x − 1 ) ( x − 2 ) d x \int_{0}^{4} x (x – 1) (x – 2) dx
الحل: الخطوة 1: فكّ توزيع الحدود نوزّع الحدود داخل التكامل:
x ( x − 1 ) ( x − 2 ) x (x – 1) (x – 2)
أولًا نضرب ( x − 1 ) ( x − 2 ) (x – 1)(x – 2)
( x − 1 ) ( x − 2 ) = x 2 − 3 x + 2 (x – 1)(x – 2) = x^2 – 3x + 2
ثم نضرب في x x
x ( x 2 − 3 x + 2 ) = x 3 − 3 x 2 + 2 x x(x^2 – 3x + 2) = x^3 – 3x^2 + 2x
الخطوة 2: حساب التكامل نحسب تكامل كل حد على حدة:
∫ 0 4 ( x 3 − 3 x 2 + 2 x ) d x \int_{0}^{4} (x^3 – 3x^2 + 2x) dx
نحسب تكامل كل حد:
∫ x 3 d x = x 4 4 \int x^3 dx = \frac{x^4}{4} ∫ − 3 x 2 d x = − x 3 \int -3x^2 dx = -x^3 ∫ 2 x d x = x 2 \int 2x dx = x^2
إذن التكامل يصبح:
[ x 4 4 − x 3 + x 2 ] 0 4 \left[ \frac{x^4}{4} – x^3 + x^2 \right]_{0}^{4}
الخطوة 3: التعويض بالحدود نحسب عند x = 4 x = 4
4 4 4 − 4 3 + 4 2 \frac{4^4}{4} – 4^3 + 4^2 = 256 4 − 64 + 16 = \frac{256}{4} – 64 + 16 = 64 − 64 + 16 = 16 = 64 – 64 + 16 = 16
وعند x = 0 x = 0
0 4 4 − 0 3 + 0 2 = 0 \frac{0^4}{4} – 0^3 + 0^2 = 0
إذن:
16 − 0 = 16 16 – 0 = 16
الإجابة النهائية: ∫ 0 4 x ( x − 1 ) ( x − 2 ) d x = 16 \int_{0}^{4} x (x – 1) (x – 2) dx = 16
b = 2