المجاميع العليا والسفلى و حلول السئلة الخارجية و الوزارية في الموضوع

السؤال رقم 4 هو:

“لُكِنَت $f(x) = 4$ حيث $f: [-2,5]$ جد المساحة تحت المنحني. ثم تحقق من ذلك هندسياً.”

لحل السؤال “جد المساحة تحت المنحنى للدالة $f(x) = 4$ على الفترة $[-2,5]$ ثم تحقق من ذلك هندسيًا.”، اتبع الخطوات التالية:

الخطوة 1: تحديد المساحة المطلوب حسابها

• الدالة المعطاة هي دالة ثابتة: $$f(x) = 4$$ وتعني أن قيمة $y$ تساوي 4 لكل $x$ في الفترة $[-2,5]$.
• الفترة المعطاة هي $-2, 5$، أي أن التكامل سيكون ضمن هذه الحدود.

الخطوة 2: حساب التكامل المحدد

المساحة تحت المنحنى تُحسب باستخدام التكامل المحدود:

$$A = \int_{-2}^{5} 4 \,dx$$

نقوم بحساب التكامل:

$$A = 4 \int_{-2}^{5} dx$$ $$A = 4 [ x ]_{-2}^{5}$$ $$A = 4 \times (5 – (-2))$$ $$A = 4 \times 7 = 28$$

إذن، المساحة تحت المنحنى تساوي 28 وحدة مربعة.

الخطوة 3: التحقق من الحل هندسيًا

• بما أن الدالة ثابتة، فإن التمثيل البياني لها يكون خطًا أفقيًا عند $y = 4$.
• المساحة المطلوبة هي المساحة المحصورة بين هذا الخط الأفقي والمحور $x$ في الفترة $[-2,5]$.
• الشكل الهندسي لهذه المساحة هو مستطيل طوله يساوي طول الفترة: $$\text{الطول} = 5 – (-2) = 7$$ وعرضه هو قيمة الدالة الثابتة: $$\text{العرض} = 4$$
• مساحة المستطيل هي: $$\text{المساحة} = \text{الطول} \times \text{العرض} = 7 \times 4 = 28$$
• وهو نفس الناتج الذي حصلنا عليه باستخدام التكامل.

النتيجة النهائية

المساحة تحت المنحنى تساوي 28 وحدة مربعة، وتحققنا من ذلك هندسيًا باستخدام قانون مساحة المستطيل.

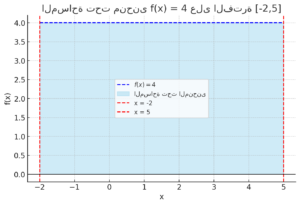
تم الآن عرض جدول القيم للدالة $f(x) = 4$ على الفترة $[-2,5]$ بالإضافة إلى الرسم البياني الذي يوضح المساحة تحت المنحنى.

• الخط الأزرق المتقطع يمثل الدالة الثابتة $f(x) = 4$.
• المساحة المظللة باللون الأزرق الفاتح تمثل المساحة المحصورة تحت المنحنى.
• الخطوط الحمراء المتقطعة تمثل حدود الفترة عند $x = -2$ و $x = 5$.

بهذه الطريقة، تحققنا من المساحة باستخدام التكامل والحساب الهندسي. 😊

السؤال الرقم 5 هو:

“لُكِنَت $f(x) = x^2 + 1$ حيث $f: [1,4]$، باستخدام التجزئة $O = \{1,2,3,4\}$، جد قيمة التكامل:

$$\int_{1}^{4} f(x) \,dx$$

لحل السؤال “جد قيمة التكامل $\int_{1}^{4} f(x) dx$ حيث $f(x) = x^2 + 1$ باستخدام التجزئة $O = \{1,2,3,4\}$“، نتبع الخطوات التالية:

الخطوة 1: تعريف التكامل باستخدام التجزئة

لدينا الفترة $[1,4]$ والتجزئة $O = \{1,2,3,4\}$، أي أن التقسيم يتم عند النقاط:

$$x_0 = 1, \quad x_1 = 2, \quad x_2 = 3, \quad x_3 = 4$$

كل جزء له عرض ثابت:

$$\Delta x = x_i – x_{i-1} = 2 – 1 = 1$$

نستخدم مجاميع داربو العليا أو السفلى لحساب التكامل باستخدام التجزئة.

الخطوة 2: حساب قيمة الدالة عند نقاط التقسيم

نحسب قيم الدالة $f(x) = x^2 + 1$ عند النقاط المعطاة:

الخطوة 3: حساب التكامل باستخدام التجزئة

بما أن التجزئة تعطينا مستطيلات عرضها $\Delta x = 1$، فإن تقريب التكامل باستخدام مجموع ريمان يكون:

$$\sum_{i=1}^{n} f(x_i^*) \Delta x$$

نستخدم قيم $f(x)$ عند النقاط المعطاة:

$$A \approx (f(1) + f(2) + f(3)) \cdot \Delta x$$

لأن النقاط 1، 2، 3 تُستخدم لحساب القيم في المستطيلات.

$$A \approx (2 + 5 + 10) \times 1$$ $$A = 17$$

الخطوة 4: حساب التكامل الحقيقي لمقارنة النتائج

نحسب التكامل الحقيقي للدالة $f(x) = x^2 + 1$:

$$\int (x^2 + 1) dx = \frac{x^3}{3} + x$$

نطبق حدود التكامل من $1$ إلى $4$:

$$\left[ \frac{x^3}{3} + x \right]_{1}^{4}$$ $$= \left( \frac{4^3}{3} + 4 \right) – \left( \frac{1^3}{3} + 1 \right)$$ $$= \left( \frac{64}{3} + 4 \right) – \left( \frac{1}{3} + 1 \right)$$ $$= \left( \frac{64}{3} + \frac{12}{3} \right) – \left( \frac{1}{3} + \frac{3}{3} \right)$$ $$= \left( \frac{76}{3} \right) – \left( \frac{4}{3} \right)$$ $$= \frac{72}{3} = 24$$

النتيجة النهائية

• باستخدام التجزئة، حصلنا على $A \approx 17$.
• باستخدام التكامل الحقيقي، المساحة الفعلية $24$.
• كلما زادت عدد نقاط التقسيم، اقتربت القيمة المحسوبة من القيمة الفعلية $24$.

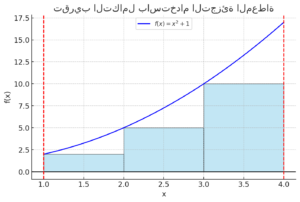
هذا هو الرسم البياني الذي يوضح تقريب التكامل باستخدام التجزئة المعطاة $O = \{1,2,3,4\}$ للدالة $f(x) = x^2 + 1$.

• الخط الأزرق يمثل منحنى الدالة $f(x) = x^2 + 1$.
• المستطيلات المظللة بالأزرق الفاتح تمثل المساحة التي يتم حسابها باستخدام التجزئة، حيث يعتمد كل مستطيل على قيمة الدالة عند نقاط التقسيم.
• الخطوط الحمراء المتقطعة عند $x=1$ و $x=4$ تحدد حدود الفترة التي يتم التكامل عليها.

هذا الرسم يوضح كيفية استخدام مجاميع ريمان لحساب المساحة تحت المنحنى، وكلما زاد عدد التقسيمات، زادت دقة التقريب. 😊

السؤال الرقم 7 هو:

“س7: لُكِنَت $f(x) = 3x – x^2$ حيث $f: [0,4]$، باستخدام التجزئة $O = \{0,1,3,4\}$، جد كلاً من المجموع الأعلى $U(O, f)$ والمجموع الأسفل $L(O, f)$.”

حل السؤال: حساب المجاميع العليا والسفلى باستخدام التجزئة

لدينا الدالة:

$$f(x) = 3x – x^2$$

على الفترة $[0,4]$ مع التجزئة $O = \{0,1,3,4\}$.

الخطوة 1: تحديد فترات التجزئة

بما أن التجزئة المعطاة هي:

$$O = \{0,1,3,4\}$$

فإن الفترات الناتجة هي:

1. الفترة الأولى: $[0,1]$
2. الفترة الثانية: $[1,3]$
3. الفترة الثالثة: $[3,4]$

نحسب طول كل فترة:

$$\Delta x_1 = 1 – 0 = 1, \quad \Delta x_2 = 3 – 1 = 2, \quad \Delta x_3 = 4 – 3 = 1$$

الخطوة 2: حساب قيم الدالة عند نقاط التجزئة

نحسب قيم الدالة عند النقاط $x = 0,1,3,4$:

الخطوة 3: حساب المجموع الأعلى $U(O,f)$

المجموع الأعلى يُحسب بأخذ القيم العظمى للدالة داخل كل فترة فرعية ثم ضربها في طول الفترة:

1. الفترة $[0,1]$:
   • القيم: $f(0) = 0$، $f(1) = 2$
   • القيمة العظمى: $M_1 = 2$
   • المساحة: $M_1 \cdot \Delta x_1 = 2 \times 1 = 2$
2. الفترة $[1,3]$:
   • القيم: $f(1) = 2$، $f(3) = 0$
   • القيمة العظمى: $M_2 = 2$
   • المساحة: $M_2 \cdot \Delta x_2 = 2 \times 2 = 4$
3. الفترة $[3,4]$:
   • القيم: $f(3) = 0$، $f(4) = -4$
   • القيمة العظمى: $M_3 = 0$
   • المساحة: $M_3 \cdot \Delta x_3 = 0 \times 1 = 0$

حساب المجموع الأعلى:

$$U(O,f) = 2 + 4 + 0 = 6$$

الخطوة 4: حساب المجموع الأسفل $L(O,f)$

المجموع الأسفل يُحسب بأخذ القيم الدنيا للدالة داخل كل فترة فرعية ثم ضربها في طول الفترة:

1. الفترة $[0,1]$:
   • القيم: $f(0) = 0$، $f(1) = 2$
   • القيمة الصغرى: $m_1 = 0$
   • المساحة: $m_1 \cdot \Delta x_1 = 0 \times 1 = 0$
2. الفترة $[1,3]$:
   • القيم: $f(1) = 2$، $f(3) = 0$
   • القيمة الصغرى: $m_2 = 0$
   • المساحة: $m_2 \cdot \Delta x_2 = 0 \times 2 = 0$
3. الفترة $[3,4]$:
   • القيم: $f(3) = 0$، $f(4) = -4$
   • القيمة الصغرى: $m_3 = -4$
   • المساحة: $m_3 \cdot \Delta x_3 = (-4) \times 1 = -4$

حساب المجموع الأسفل:

$$L(O,f) = 0 + 0 – 4 = -4$$

النتيجة النهائية

• المجموع الأعلى: $U(O, f) = 6$
• المجموع الأسفل: $L(O, f) = -4$

التحليل

• الفرق بين المجموع الأعلى والأسفل $U(O,f) – L(O,f) = 6 – (-4) = 10$ يُشير إلى أن الدالة ليست ثابتة وتزداد ثم تنخفض، مما يجعل التكامل أكثر دقة عند استخدام تجزئة أصغر.
• يمكن تحسين دقة التقريب باستخدام تجزئة أصغر حجمًا، مما يؤدي إلى تقليل الفرق بين المجاميع.

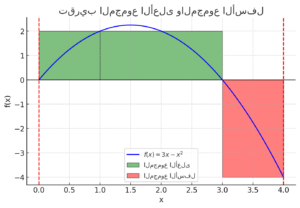
هذا هو الرسم البياني الذي يوضح المجموع الأعلى والمجموع الأسفل للدالة $f(x) = 3x – x^2$ باستخدام التجزئة $O = \{0,1,3,4\}$.

• الخط الأزرق يمثل منحنى الدالة $f(x)$.
• المستطيلات الخضراء تمثل المجموع الأعلى $U(O, f)$، حيث يتم أخذ القيم العظمى لكل فترة.
• المستطيلات الحمراء تمثل المجموع الأسفل $L(O, f)$، حيث يتم أخذ القيم الدنيا لكل فترة.
• الخطوط الحمراء المتقطعة تحدد حدود الفترة عند $x = 0$ و $x = 4$.