إيجاد المساحة بين المنحنيين
(الدوال المثلثية) – امثلة الاسئلة الوزارية
السؤال :
جد المساحة المحددة بين منحني الدالتين
و
وعلى الفترة .
خطوات حل المسألة: إيجاد المساحة المحددة بين منحني الدالتين
و
في الفترة
الخطوة 1: إيجاد نقاط التقاطع بين الدالتين
لحساب المساحة، نحتاج إلى معرفة متى تكون الدالتان متساويتين، أي حل المعادلة:
نستخدم متطابقة ضعف الزاوية:
وبالتالي تصبح المعادلة:
نحلل المعادلة:
أي أن:
- →
- →
- من جدول القيم المثلثية، نجد أن في الفترة المطلوبة.
إذن، نقاط التقاطع في الفترة هي:
الخطوة 2: تقسيم التكامل إلى جزأين
المساحة تُحسب باستخدام التكامل المحدد لمقدار الفرق بين الدالتين:
حيث نأخذ الفرق بناءً على أي الدالتين تكون الأعلى في كل فترة:
- في يكون .
- في يكون .
الخطوة 3: حساب التكامل لكل جزء
1. التكامل الأول:
إذن:
بحساب القيم عند و ، نحصل على:
2. التكامل الثاني:
بنفس الطريقة:
بعد حساب القيم، نجد أن النتيجة هي .
الخطوة 4: حساب المساحة النهائية
إذن، المساحة المحصورة بين المنحنيين هي وحدة مربعة.
ملخص الحل
- وجدنا نقاط التقاطع عند و .
- قسمنا التكامل إلى جزأين حسب ترتيب المنحنيين.
- حسبنا كل تكامل بشكل منفصل.
- جمعنا القيم المطلقة للحصول على المساحة الكلية .
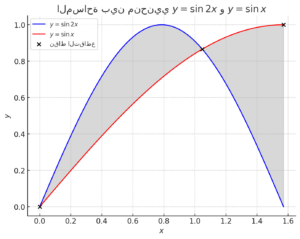 مساحة بين منحنيي
مساحة بين منحنيي
هذا هو الرسم البياني لمنحنيي (باللون الأزرق) و (باللون الأحمر) على الفترة .
- تم تظليل المساحة بين المنحنيين (بالعتمة الرمادية) والتي تمثل المساحة المطلوبة.
- النقاط السوداء تمثل نقاط التقاطع عند ، ، و .
السؤال الوزاري:
جد المساحة المحددة بين منحني الدالتين
و
وعلى الفترة .
خطوات حل المسألة: إيجاد المساحة المحددة بين منحني الدالتين
و
على الفترة
الخطوة 1: إيجاد نقاط التقاطع بين الدالتين
لحساب المساحة، نحتاج إلى معرفة متى تتساوى الدالتان، أي حل المعادلة:
نرتب المعادلة:
نقوم بإخراج العامل المشترك:
إذن لدينا حلّان:
إذن، نقاط التقاطع في الفترة هي:
الخطوة 2: تحديد الدالة العلوية والسفلية
لإيجاد المساحة، يجب معرفة أي الدالتين تقع فوق الأخرى في الفترة .
- نلاحظ أن لأن وبالتالي أصغر أو يساوي .
إذن، التكامل يكون على الفرق بين الدالتين:
الخطوة 3: حساب التكامل
تبسيط التكامل
نستخدم المتطابقة المثلثية:
وبالتالي يصبح التكامل:
حساب التكاملات الثلاثة:
-
-
نستخدم المتطابقة :
نحسب كل جزء:
إذن:
الخطوة 4: حساب المساحة النهائية
إذن، المساحة المحصورة بين المنحنيين تساوي أو تقريبًا 0.215 وحدة مربعة.
ملخص الحل
- إيجاد نقاط التقاطع عند و .
- تحديد الدالة العلوية والسفلية ( أعلى من ).
- إعداد التكامل:
- حساب التكاملات الفرعية للحصول على النتيجة:
الرسم البياني
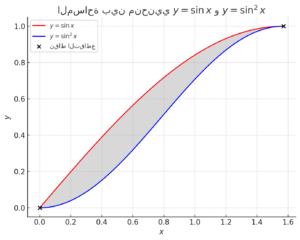
هذا هو الرسم البياني لمنحنيي (باللون الأحمر) و (باللون الأزرق) على الفترة .
- المنطقة المظللة باللون الرمادي تمثل المساحة المحصورة بين المنحنيين، وهي المساحة المطلوبة في المسألة.
- النقاط السوداء تمثل نقاط التقاطع عند و .


