اسئلة و تمارين حول تكاملات المسافة
السؤال رقم 2 هو:
جسم يتحرك على خط مستقيم بسرعته m/s
1️⃣ جد المسافة المقطوعة في الفترة .
2️⃣ جد الإزاحة المقطوعة في الفترة .
لحل السؤال، سنستخدم التكامل لتحديد الإزاحة والمسافة المقطوعة بناءً على دالة السرعة المعطاة:
أولًا: حساب المسافة المقطوعة في الفترة
المسافة المقطوعة تُحسب بأخذ القيمة المطلقة للسرعة عند التكامل:
ولكن يجب أولًا إيجاد الجذور حيث تكون السرعة سالبة لتحديد المناطق التي تحتاج إلى الفصل.
نحلل:
بما أن ليس ضمن الفترة ، نتحقق من إشارة بين 2 و 4:
بما أن السرعة موجبة في الفترة ، نحسب التكامل مباشرة:
نحسب التكامل:
نقيمه بين 2 و 4:
إذًا المسافة المقطوعة = 26 مترًا.
ثانيًا: حساب الإزاحة في الفترة
الإزاحة هي التكامل المباشر بدون القيم المطلقة:
نحسب التكامل:
إذًا الإزاحة المقطوعة = 65 مترًا.
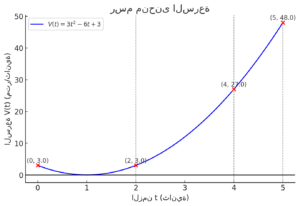 رسم منحنى السرعة
رسم منحنى السرعة
في الرسم أعلاه، يظهر منحنى السرعة باللون الأزرق. كما تم تحديد النقاط الزمنية المهمة (عند ) باللون الأحمر مع إحداثياتها.
- الخطوط العمودية المتقطعة تشير إلى الفترات الزمنية المطلوبة في المسألة.
- الإزاحة هي المساحة تحت المنحنى بين و .
- المسافة المقطوعة تحسب من التكامل المطلق للسرعة بين و .
يظهر أن السرعة موجبة في الفترة المدروسة، مما يجعل التكامل المباشر يمثل المسافة بدون الحاجة لأخذ القيم المطلقة.
السؤال هو:
س3 جسم يتحرك على خط مستقيم بتعجيل مقداره ، فإذا كانت سرعته قد أصبحت بعد مرور ثوانٍ من بدء الحركة، جد:
- المسافة المقطوعة خلال الثانية الثالثة.
- بعده عن نقطة بدء الحركة بعد مرور ثوانٍ.
حل السؤال:
معطيات السؤال:
- التعجيل (a):
- السرعة النهائية (v):
- الزمن (t): ثوانٍ
- السرعة الابتدائية (u): مجهولة
أولاً: إيجاد السرعة الابتدائية ()
نستخدم معادلة الحركة:
(1) إيجاد المسافة المقطوعة في الثانية الثالثة
المسافة المقطوعة خلال الثانية تُحسب بالعلاقة:
عند :
(2) إيجاد المسافة المقطوعة بعد 3 ثوانٍ
نستخدم معادلة الإزاحة:
الإجابات النهائية:
- المسافة المقطوعة في الثانية الثالثة = متر
- البعد عن نقطة بدء الحركة بعد مرور 3 ثوانٍ = متر
السؤال 4 هو:
جسم يتحرك على خط مستقيم بتعجيل، فإذا كانت العجلة مقدارها
وكانت سرعته قد أصبحت
بعد مرور
من بدء الحركة، جد:
- السرعة عند .
- المسافة المقطوعة في الفترة .
- الإزاحة بعد مضي ثوانٍ من بدء الحركة.
المعطيات:
- العجلة المتغيرة:
- السرعة النهائية بعد ثوانٍ:
- المطلوب:
- إيجاد السرعة عند .
- حساب المسافة المقطوعة في الفترة .
- حساب الإزاحة بعد ثوانٍ.
1- إيجاد السرعة عند :
بما أن العجلة تتغير مع الزمن، يمكن حساب السرعة باستخدام التكامل:
لإيجاد ثابت التكامل ، نستخدم المعطى أن عند :
إذن معادلة السرعة هي:
حساب السرعة عند :
2- حساب المسافة المقطوعة في الفترة :
المسافة المقطوعة تُحسب من تكامل السرعة:
نحسب المسافة بين و :
3- حساب الإزاحة بعد 10 ثوانٍ:
لحساب الإزاحة، نستخدم معادلة الموضع:
نحسب :
الإجابات النهائية:
- السرعة عند :
- المسافة المقطوعة في الفترة :
- الإزاحة بعد ثوانٍ:

