التكامل المحدد / الدالة المقابلة / محاضرة 19

النظرية الأساسية للتكامل – “الدالة المقابلة”

مقدمة

تعد النظرية الأساسية للتكامل واحدة من أهم النظريات في حساب التفاضل والتكامل، حيث تربط بين عمليتي التكامل والتفاضل. ومن أهم المفاهيم المتعلقة بها هو “الدالة المقابلة” والتي تلعب دورًا محوريًا في فهم سلوك التكاملات وإيجاد الحلول للعديد من المسائل الرياضية.

1. تعريف الدالة المقابلة

إذا كانت $f(x)$ دالة مستمرة على فترة معينة، فإننا نعرف الدالة المقابلة $F(x)$ على النحو التالي:

$$F(x) = \int_{a}^{x} f(t) \, dt$$

حيث تمثل $F(x)$ مجموع المساحة تحت المنحنى للدالة $f(x)$ بدءًا من نقطة ثابتة $a$ وحتى النقطة المتغيرة $x$.

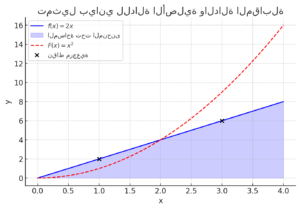
هذا الرسم البياني يوضح العلاقة بين الدالة الأصلية $f(x) = 2x$ والدالة المقابلة $F(x) = x^2$:

• الخط الأزرق يمثل الدالة الأصلية $f(x) = 2x$.
• المساحة المظللة باللون الأزرق تمثل التكامل المحدد، أي المساحة المتراكمة تحت المنحنى.
• الخط الأحمر المتقطع يمثل الدالة المقابلة $F(x) = x^2$، والتي تعبر عن تكامل $f(x)$.

الرسم يوضح كيف أن الدالة المقابلة $F(x)$ تعبر عن المساحة تحت المنحنى، وعند اشتقاقها نحصل على $f(x)$.

2. النظرية الأساسية للتكامل

تنص النظرية الأساسية للتكامل على أنه إذا كانت $f(x)$ دالة مستمرة على فترة مغلقة $[a, b]$، وكان $F(x)$ دالة مقابلة لها كما هو معرف أعلاه، فإن:

الجزء الأول من النظرية:

الدالة $F(x)$ معرفة على الفترة $[a, b]$ وهي قابلة للاشتقاق، كما أن:

$$F'(x) = f(x)$$

وهذا يعني أن التفاضل والتكامل عمليتان عكسيتان لبعضهما.

الجزء الثاني من النظرية:

إذا كانت $F(x)$ دالة أصلية لـ $f(x)$، فإن التكامل المحدد يمكن حسابه باستخدام:

$$\int_{a}^{b} f(x) \, dx = F(b) – F(a)$$

حيث $F(x)$ هي أي دالة أصلية للدالة $f(x)$.

3. تفسير هندسي

• تمثل الدالة المقابلة $F(x)$ المساحة المتراكمة تحت منحنى الدالة $f(x)$.
• عند اشتقاق $F(x)$، نحصل على $f(x)$، أي أن المعدل اللحظي لتغير المساحة المتراكمة يعطينا قيمة الدالة الأصلية.

4. تطبيقات على الدالة المقابلة

(أ) حساب المساحات

يمكن استخدام الدالة المقابلة لحساب المساحة تحت منحنى الدالة بين نقطتين معينتين، كما هو موضح في:

$$\int_{a}^{b} f(x) \, dx = F(b) – F(a)$$

(ب) حل المعادلات التفاضلية

بما أن التكامل هو العملية العكسية للتفاضل، فإنه يمكن استخدام الدالة المقابلة لحل العديد من المعادلات التفاضلية وإيجاد الحلول العامة.

(ج) الفيزياء والهندسة

• تستخدم في حساب الإزاحة من السرعة، حيث تكون الإزاحة هي تكامل السرعة.
• في التحليل الكهربائي، حيث يتم استخدام التكامل لحساب الشحنة المتدفقة عبر الدوائر الكهربائية.

5. مثال عملي

مثال:

إذا كانت $f(x) = 2x$، فلنحسب الدالة المقابلة لها:

$$F(x) = \int 2x \, dx = x^2 + C$$

ولحساب التكامل المحدد من $x = 1$ إلى $x = 3$:

$$\int_{1}^{3} 2x \, dx = F(3) – F(1)$$ $$= (3^2) – (1^2) = 9 – 1 = 8$$

الخلاصة

• الدالة المقابلة هي دالة تمثل التكامل غير المحدد لدالة أخرى.
• النظرية الأساسية للتكامل تربط بين عمليتي التكامل والتفاضل، حيث يوضح الجزء الأول أن التكامل غير المحدد هو عكس التفاضل، بينما الجزء الثاني يحدد كيفية حساب التكامل المحدد.
• لها تطبيقات واسعة في مجالات متعددة مثل الرياضيات والفيزياء والهندسة.

💡 فهم النظرية الأساسية للتكامل يسهل التعامل مع العديد من المفاهيم الرياضية الأخرى، ويجعل من السهل تحليل العلاقات بين الدوال المختلفة.

السؤال :

إذا كانت $f$ دالة مستمرة على $[0, \frac{\pi}{2}]$ حيث أن:

$$F(x) = \sin x$$

هي دالة مقابلة للدالة $f$.

جد:

$${\int }_0^{\frac{\pi }{2}}F(x)dx$$

لحساب التكامل المحدد:

$$\int_{0}^{\frac{\pi}{2}} \sin x \, dx$$

نقوم بحساب التكامل غير المحدد أولًا:

$$\int \sin x \, dx = -\cos x$$

ثم نطبق حدود التكامل:

$$\left[-\cos x \right]_{0}^{\frac{\pi}{2}}$$ $$= -\cos\left(\frac{\pi}{2}\right) + \cos(0)$$ $$= -0 + 1 = 1$$

إذن، قيمة التكامل هي:

$$1$$

السؤال :

1. أثبت أن الدالة $F(x)$ هي دالة مقابلة للدالة $f(x)$.

   حيث:

   $$F(x) = \frac{1}{2} \sin 2x$$ $$f(x) = \cos 2x$$مع مجال الدالتين $[0, 2\pi]$.

2. ثم أوجد:

   $$\int_{0}^{2\pi} \cos 2x \, dx$$

إثبات أن $F(x)$ دالة مقابلة لـ $f(x)$

لدينا:

$$F(x) = \frac{1}{2} \sin 2x$$

نحسب المشتقة:

$$F'(x) = \frac{1}{2} \cdot \cos 2x \cdot 2$$ $$= \cos 2x$$

وهذا مطابق لـ $f(x)$، أي:

$$F'(x) = f(x)$$

إذن، $F(x)$ دالة مقابلة لـ $f(x)$. ✅

حساب التكامل المحدد

$$\int_{0}^{2\pi} \cos 2x \, dx$$

نحسب التكامل غير المحدد:

$$\int \cos 2x \, dx = \frac{\sin 2x}{2}$$

ثم نطبق حدود التكامل من $0$ إلى $2\pi$:

$$\left[ \frac{\sin 2x}{2} \right]_{0}^{2\pi}$$ $$= \frac{\sin (4\pi)}{2} – \frac{\sin (0)}{2}$$ $$= \frac{0}{2} – \frac{0}{2} = 0$$

إذن، قيمة التكامل هي:

$$0$$

$$\int_{0}^{\frac{\pi}{2}} F(x) \, dx$$