المحاضرة 2/ القطع المكافئ
القطوع المخروطية – القطع المكافئ
تعريف القطع المكافئ: القطع المكافئ هو أحد أنواع القطوع المخروطية، وهو مجموعة نقاط المستوى التي تكون متساوية البعد عن نقطة ثابتة تسمى البؤرة وخط ثابت يسمى الدليل.
معادلة القطع المكافئ:
- عندما يكون محور التماثل أفقيًا:
- الرأس:
- البؤرة:
- الدليل:
- اتجاه الفتحة:
- إذا كان يتجه نحو اليمين.
- إذا كان يتجه نحو اليسار.
- عندما يكون محور التماثل رأسيًا:
- الرأس:
- البؤرة:
- الدليل:
- اتجاه الفتحة:
- إذا كان يتجه للأعلى.
- إذا كان يتجه للأسفل.
إيجاد معادلة القطع المكافئ:
لإيجاد معادلة القطع المكافئ الذي رأسه نقطة الأصل وبؤرته :
- الرأس:
- البؤرة:
- بما أن البؤرة تقع على المحور الأفقي، فإن معادلة القطع المكافئ تأخذ الشكل:
حيث هو بعد البؤرة عن الرأس:
بالتعويض:
أي:
صور توضيحية:
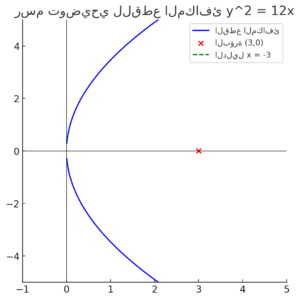
إذا كنت بحاجة إلى المزيد من الشروحات أو التمارين، لا تتردد في طلب ذلك!
