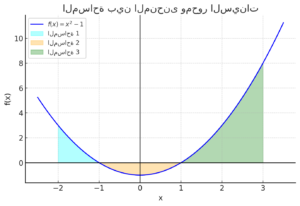
التكامل – ايجاد المساحة بين منحني الدالة و محور السينات

ايجاد المساحة بين منحني الدالة و محور السينات

التكامل – إيجاد المساحة بين منحنى الدالة ومحور السينات

التكامل هو أداة رياضية تُستخدم لحساب المساحة تحت المنحنيات، وهو أحد أهم التطبيقات في علم التفاضل والتكامل. عندما يكون لدينا دالة $f(x)$، يمكننا إيجاد المساحة بين منحنى هذه الدالة ومحور السينات (محور $x$) باستخدام التكامل المحدد.

1. القاعدة الأساسية لإيجاد المساحة باستخدام التكامل

إذا كانت الدالة $f(x)$ معرفة ومحددة على الفترة $[a, b]$، فإن المساحة المحصورة بين منحنى الدالة ومحور $x$ تُحسب بواسطة التكامل المحدد:

$$A = \int_{a}^{b} f(x) \, dx$$

حيث:

• $a, b$ هما حدود التكامل (النقاط التي تُحدد نطاق الحساب).
• $f(x)$ هي الدالة التي تمثل المنحنى.
• $dx$ يرمز إلى متغير التكامل، وهو يشير إلى مجموع المساحات الصغيرة تحت المنحنى.

2. الحالات المختلفة لحساب المساحة

أ. إذا كانت $f(x)$ موجبة على $[a, b]$

إذا كانت $f(x)$ أكبر من الصفر في الفترة $[a, b]$، فإن المساحة بين المنحنى والمحور السيني تساوي قيمة التكامل مباشرة:

$$A = \int_{a}^{b} f(x) \, dx$$

ب. إذا كانت $f(x)$ سالبة على $[a, b]$

إذا كان منحنى الدالة يقع أسفل محور $x$ في الفترة $[a, b]$، فإن قيمة التكامل ستكون سالبة، ولكن المساحة دائمًا موجبة، لذا نأخذ القيمة المطلقة:

$$A = \left| \int_{a}^{b} f(x) \, dx \right|$$

ج. إذا كانت $f(x)$ تغير الإشارة في الفترة $[a, b]$

إذا كانت $f(x)$ تتغير بين القيم الموجبة والسالبة، فيجب تقسيم التكامل عند النقاط التي تقطع فيها الدالة محور السينات، ثم حساب المساحة في كل جزء على حدة وأخذ القيم المطلقة:

$$A = \left| \int_{a}^{c} f(x) \, dx \right| + \left| \int_{c}^{b} f(x) \, dx \right|$$

حيث $c$ هو الجذر الذي يجعل $f(c) = 0$.

3. أمثلة محلولة

مثال 1: حساب المساحة تحت منحنى $f(x) = x^2$ بين $x = 0$ و$x = 2$

$$A = \int_{0}^{2} x^2 \, dx$$

نحسب التكامل:

$$A = \left[ \frac{x^3}{3} \right]_{0}^{2}$$ $$A = \frac{2^3}{3} – \frac{0^3}{3} = \frac{8}{3}$$

مثال 2: حساب المساحة بين منحنى $f(x) = x^3 – x$ ومحور $x$ في الفترة $[-1, 1]$

1. نجد الجذور: $x^3 – x = 0$ يعطي $x(x^2 – 1) = 0$، أي $x = -1, 0, 1$.
2. نقسم التكامل إلى جزأين:

$$A = \left| \int_{-1}^{0} (x^3 – x) \, dx \right| + \left| \int_{0}^{1} (x^3 – x) \, dx \right|$$

3. نحسب كل تكامل ونأخذ القيمة المطلقة للحصول على المساحة الكلية.

4. استنتاجات هامة

• التكامل المحدد يعطي “الإجمالي الجبري” للمساحة، وليس المساحة الفعلية دائمًا، لذا نأخذ القيم المطلقة عند الحاجة.
• المساحات الواقعة أسفل محور السينات تحتاج إلى التصحيح عبر القيم المطلقة.
• تقسيم المساحة عند النقاط الحرجة (جذور الدالة) ضروري في بعض الحالات.

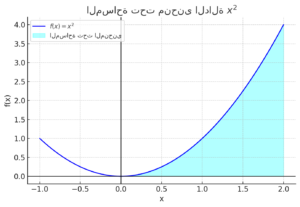
هذا الرسم البياني يوضح منحنى الدالة $f(x) = x^2$ مع تظليل المساحة الواقعة بين المنحنى ومحور السينات في الفترة $[0,2]$، والتي يمكن حسابها باستخدام التكامل المحدد.

حل سؤال إيجاد المساحة المحصورة بين منحنى الدالة $f(x) = x^3 – 4x$ ومحور السينات في الفترة $[-2,2]$

الخطوة 1: إيجاد جذور الدالة (نقاط التقاطع مع محور السينات)

لحساب المساحة، نحدد أولاً القيم التي تجعل $f(x) = 0$:

$$x^3 – 4x = 0$$

نأخذ عامل مشترك:

$$x(x^2 – 4) = 0$$

نحلل الفرق بين المربعين:

$$x(x – 2)(x + 2) = 0$$

إذًا الجذور هي:

$$x = -2, 0, 2$$

هذه هي النقاط التي تقطع عندها الدالة محور السينات.

الخطوة 2: تقسيم التكامل وفقاً لجذور الدالة

بما أن الجذور تفصل التكامل إلى أجزاء حيث قد تتغير إشارة الدالة، فإننا نقسم التكامل إلى جزأين:

1. المساحة بين $x = -2$ و $x = 0$
2. المساحة بين $x = 0$ و $x = 2$

نحسب التكامل لكل جزء على حدة.

الخطوة 3: حساب التكامل لكل جزء

نحسب التكامل:

$$A_1 = \int_{-2}^{0} (x^3 – 4x) \, dx$$

و

$$A_2 = \int_{0}^{2} (x^3 – 4x) \, dx$$

باستخدام التكامل:

$$\int (x^3 – 4x) \, dx = \frac{x^4}{4} – 2x^2$$

نطبق الحدود على كل تكامل.

حساب $A_1$:

$$A_1 = \left[ \frac{x^4}{4} – 2x^2 \right]_{-2}^{0}$$

عند $x = 0$:

$$\frac{0^4}{4} – 2(0)^2 = 0$$

عند $x = -2$:

$$\frac{(-2)^4}{4} – 2(-2)^2 = \frac{16}{4} – 2(4) = 4 – 8 = -4$$

إذًا:

$$A_1 = 0 – (-4) = 4$$

حساب $A_2$:

$$A_2 = \left[ \frac{x^4}{4} – 2x^2 \right]_{0}^{2}$$

عند $x = 2$:

$$\frac{(2)^4}{4} – 2(2)^2 = \frac{16}{4} – 2(4) = 4 – 8 = -4$$

عند $x = 0$:

$$0$$

إذًا:

$$A_2 = -4 – 0 = -4$$

لكن المساحة لا تكون سالبة، لذا نأخذ القيمة المطلقة:

$$A_2 = 4$$

الخطوة 4: حساب المساحة الكلية

المساحة الكلية هي مجموع القيم المطلقة للمساحتين:

$$A = |A_1| + |A_2|$$ $$A = 4 + 4 = 8$$

النتيجة النهائية

المساحة المحصورة بين منحنى الدالة $f(x) = x^3 – 4x$ ومحور السينات في الفترة $[-2,2]$ هي:

8 وحدات

الجذور التي تجعل $f(x) = 0$ هي $x = -2, 0, 2$.
بما أن هذه الجذور تقع داخل الفترة $[-2,2]$، سنقوم بتقسيم التكامل إلى جزأين:

1. التكامل من $x = -2$ إلى $x = 0$.
2. التكامل من $x = 0$ إلى $x = 2$.

الخطوة التالية هي حساب التكامل لكل جزء وأخذ القيمة المطلقة. سأكمل الحساب الآن.

المساحة المحددة بين منحنى الدالة $f(x) = x^3 – 4x$ ومحور السينات في الفترة $[-2,2]$ هي 8 وحدات مربعة.

سأقوم أيضًا برسم المنحنى مع تظليل المساحة المطلوبة.

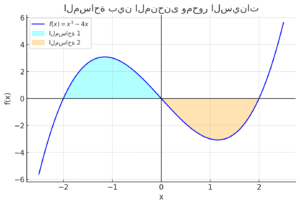
هذا الرسم البياني يوضح منحنى الدالة $f(x) = x^3 – 4x$ مع تظليل المساحات الواقعة بين المنحنى ومحور السينات في الفترة $[-2,2]$.

• المساحة المظللة باللون الأزرق الفاتح تمثل الجزء الموجب.
• المساحة المظللة باللون البرتقالي تمثل الجزء السالب (وأخذنا قيمتها المطلقة لحساب المساحة الكلية).

المساحة الكلية المحصورة بين المنحنى ومحور السينات هي 8 وحدات مربعة. 🚀

السؤال  هو:

“جد المساحة المحددة بالمنحنى $f(x) = x^2 – 1$ ومحور السينات وعلى الفترة $[-2,3]$.”

حل سؤال إيجاد المساحة المحصورة بين منحنى الدالة $f(x) = x^2 – 1$ ومحور السينات في الفترة $[-2,3]$

الخطوة 1: إيجاد جذور الدالة (نقاط التقاطع مع محور السينات)

لحساب المساحة، نحدد أولاً القيم التي تجعل $f(x) = 0$:

$$x^2 – 1 = 0$$

نحلل المعادلة:

$$(x – 1)(x + 1) = 0$$

إذًا الجذور هي:

$$x = -1, 1$$

هذه هي النقاط التي تقطع عندها الدالة محور السينات.

الخطوة 2: تقسيم التكامل وفقاً لجذور الدالة

بما أن الجذور تفصل التكامل إلى أجزاء حيث قد تتغير إشارة الدالة، فإننا نقسم التكامل إلى ثلاثة أجزاء:

1. المساحة بين $x = -2$ و $x = -1$
2. المساحة بين $x = -1$ و $x = 1$
3. المساحة بين $x = 1$ و $x = 3$

نحسب التكامل لكل جزء على حدة.

الخطوة 3: حساب التكامل لكل جزء

نحسب التكامل:

$$A_1 = \int_{-2}^{-1} (x^2 – 1) \, dx$$ $$A_2 = \int_{-1}^{1} (x^2 – 1) \, dx$$ $$A_3 = \int_{1}^{3} (x^2 – 1) \, dx$$

باستخدام التكامل:

$$\int (x^2 – 1) \, dx = \frac{x^3}{3} – x$$

نطبق الحدود على كل تكامل.

حساب $A_1$:

$$A_1 = \left[ \frac{x^3}{3} – x \right]_{-2}^{-1}$$

عند $x = -1$:

$$\frac{(-1)^3}{3} – (-1) = -\frac{1}{3} + 1 = \frac{2}{3}$$

عند $x = -2$:

$$\frac{(-2)^3}{3} – (-2) = -\frac{8}{3} + 2 = -\frac{8}{3} + \frac{6}{3} = -\frac{2}{3}$$

إذًا:

$$A_1 = \frac{2}{3} – (-\frac{2}{3}) = \frac{4}{3}$$

حساب $A_2$:

$$A_2 = \left[ \frac{x^3}{3} – x \right]_{-1}^{1}$$

عند $x = 1$:

$$\frac{(1)^3}{3} – 1 = \frac{1}{3} – 1 = -\frac{2}{3}$$

عند $x = -1$:

$$\frac{(-1)^3}{3} – (-1) = -\frac{1}{3} + 1 = \frac{2}{3}$$

إذًا:

$$A_2 = -\frac{2}{3} – \frac{2}{3} = -\frac{4}{3}$$

ولكن لأن المساحة لا تكون سالبة، نأخذ القيمة المطلقة:

$$A_2 = \frac{4}{3}$$

حساب $A_3$:

$$A_3 = \left[ \frac{x^3}{3} – x \right]_{1}^{3}$$

عند $x = 3$:

$$\frac{(3)^3}{3} – 3 = \frac{27}{3} – 3 = 9 – 3 = 6$$

عند $x = 1$:

$$\frac{(1)^3}{3} – 1 = \frac{1}{3} – 1 = -\frac{2}{3}$$

إذًا:

$$A_3 = 6 – (-\frac{2}{3}) = 6 + \frac{2}{3} = \frac{18}{3} + \frac{2}{3} = \frac{20}{3}$$

الخطوة 4: حساب المساحة الكلية

المساحة الكلية هي مجموع القيم المطلقة للمساحات الثلاثة:

$$A = |A_1| + |A_2| + |A_3|$$ $$A = \frac{4}{3} + \frac{4}{3} + \frac{20}{3}$$ $$A = \frac{28}{3}$$

النتيجة النهائية

المساحة المحصورة بين منحنى الدالة $f(x) = x^2 – 1$ ومحور السينات في الفترة $[-2,3]$ هي:

28/3